Урок 16. Функція, зворотна даною

вторник, 30 мая 2017 г.

Урок 16. Функція, зворотна даною

Відношення, зворотне даному.

ПРИКЛАД:

На малюнку відношення р між елементами множини Х і елементами множини Y задане за допомогою стрілок.

Поміняємо напрям стрілок.

Отримаємо інше відношення – відношення q між елементами множини Y і елементами множини Х.

Говорять, що q є відношення, зворотне відношенню р. У свою чергу відношення р є зворотним відношенню q.

Областю визначення відношення p є множина

{–3; –2; –1},

а областю значень – множина

{2; 3; 4; 5}

Для відношення q, зворотного відношенню р, областю визначення служить множина

{2; 3; 4; 5},

а областю значень – множина

{–3; –2; –1}.

Таким чином, область визначення і область значень взаємно-зворотних стосунків міняються ролями.

Відношення p між елементами безлічі Х і Y визначається безліччю пар:

{(–3; 2); (–2; 3); (–1; 4); (–1; 5)}

Помінявши в кожній парі місцями її елементи, отримаємо безліч пар, яким задається відношення q, зворотне р:

{(2; –3); (3; –2); (4; –1); (5; –1)}

Якщо відношення визначається деякою безліччю пар, то зворотне йому відношення визначається безліччю пар, яке отримане з першого перестановкою елементів в кожній парі.

ПРИКЛАД:

Повернемося до розглянутих вище взаємно-зворотних відношень р і q.

На малюнку побудований графік відношення р.

На малюнку побудований графік відношення q.

Побудуємо тепер графіки відношень р і q в одній і тій же системі координат.

Неважко помітити, що точки з координатами

(–3; 2) и (2; –3),

(–1; 4) и (4; –1) и т. д.,

т. е. точки, у яких абсциса першої є ординатою другий і ордината першої є абсцисою другою, симетричні відносно прямої

у = х.

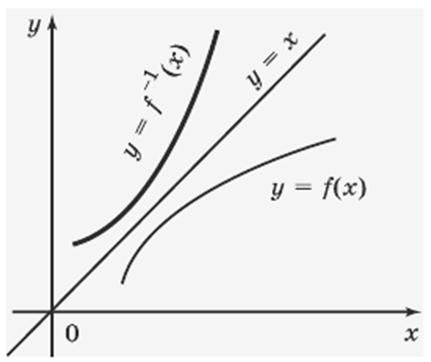
Кожній точці графіку відношення р відповідає симетрична відносно прямої у = х точка графіку відношення q, і навпаки, кожній точці графіку відношення q відповідає симетрична відносно прямої у = х точка графіку відношення р. Тому графіки відношень р і q симетричні відносно прямої у = х.

Взагалі справедлива наступна теорема:

Графіки взаємно-зворотних стосунків між числами симетричні відносно прямої у = х.

Наведемо приклади взаємно-зворотних відношень

ПРИКЛАД:

На малюнку за допомогою стрілок показано відношення <<менше>> між елементами великої кількості

А = {5; 7; 10}

В = {2; 3; 8; 12}

Зворотне йому відношення є відношенням <<більше>> між елементами великої кількості В і елементами безлічі А.

ПРИКЛАД:

Відношення <<бути дільником>> і <<бути кратним>> між натуральними числами – взаємно-зворотні відношення.

Дійсно, якщо а і b – деякі натуральні числа і а дільник b, то b кратно а, і навпаки, якщо b кратно а, те а дільник b. Наприклад, з того, що <<2 дільник 6>>, витікає, що <<6 кратно 2>>; з того, що <<24 кратно 8>>, витікає, що <<8 дільник 24>>.

Поняття функції, зворотної даної.

Якщо функція у = f(х) така, що для будь-якого значення у₀ рівняння f(х) = у₀ має відносно х єдиний корінь, то кажуть, що функція у = f(х) оборотна.

Якщо функція у = f(х) оборотна, то, висловивши х їх формули у = f(х) і змінивши потім х і у місцями, отримаємо зворотну функцію, її позначають

у = f ^-1 (х).

Приклад оборотної функції.

Приклад незворотної функції.

ПРИКЛАД:

На малюнку за допомогою стрілок задано відношення р між елементами великих кількостей А і В. Це відношення – функція, оскільки кожному елементу великої кількості А відповідає не більше за одну безліч В.

Відношення q між елементами великої кількості В і А, зворотне р, не є функцією: в множині В існує елемент (число 2), якому відповідає більше за один елемент з множини А (елементи 5 і 6).

ПРИКЛАД:

На малюнках за допомогою стрілок задано відношення f між елементами безлічі X і Y і зворотне йому відношення g між елементами безлічі Y і X.

Відношення f – функція, відношення g, зворотне f, теж функція.

Наведені приклади показують, що відношення, зворотне функції, може бути функцією, а може і не бути функцією.

Функція f називається оберненої, якщо зворотне їй відношення – функція.

В цьому випадку відношення, зворотне функції f, називають функцією, зворотною f.

Ми розглянули приклади функцій p і f, заданих за допомогою стрілок. Оборотною виявилася функція у тому випадку, коли до будь-якого елементу області її значень було проведено не більше за одну стрілку, т. е. коли кожного свого значення функції набувала тільки при одному значенні аргументу.

Функція обернена тоді і тільки тоді, коли кожного свого значення вона набуває лише при одному значенні аргументу.

Якщо функція у = f(х) визначена і зростає (зменшується) на проміжку Х і областю її значень є проміжок Y, то вона існує зворотна функція, причому зворотна функція визначена і зростає (зменшується) на Y.

Для знаходження функції, зворотної даної у = f(х), треба виразити х через у: х = g(у), а потім записати отриману функцію у загальноприйнятій формі у = g(х).

Якщо функції у = f(х) і у = g(х) є взаємно зворотними, то область визначення функції f збігається з безліччю значень функції g і, навпаки, область визначення функції g збігається з безліччю значень функції f, тобто

D(f) = E(g) і D(g) = E(f).

Всяка зростаюча функція обернена.

Функція, зворотна такою, що зростає, є такою, що зростає.

Всяка спадаюча функція обернена.

Функція, зворотна такою, що убуває, є такою, що убуває.

Якщо деяке відношення f задане рівнянням з двома змінними х і у, то для завдання рівнянням відношення, зворотного f, досить в цьому рівнянні поміняти позначення х на у і у на х.

ПРИКЛАД:

Функція f, задана формулою

у = –2х + 3,

що спадає. Тому вона обернена. Зворотна їй функція також спадає.

Щоб задати формулою функцію, зворотну f, поміняємо в рівнянні

у = –2х + 3,

позначення х на у і у на х. Отримаємо рівняння

х = –2у + 3

Зазвичай при завданні функції рівнянням зі змінними х і у змінну у виражають через змінну х.

В даному випадку маємо:

2у = –х + 3,

у = –0,5х + 1,5.

Ми отримали формулу, якій задається функція, зворотна f.

ПРИКЛАД:

Нехай дано функцію:

у = 3х – 2.

Якщо виразити х через у і в одержаній рівності заміст х написати у, а замість у написати х, будемо мати:

Це є функція, обернена до даної. Дану функцію також можна назвати оберненою по відношенню до одержаної. Ці функції взаємно обернені.

Не для кожної функції існує обернена.

ПРИКЛАД:

Для функції, заданої рівністю:

у = х²

На

(–∞; +∞ ),

оберненої не існує. А для функції:

у = х²

заданої на проміжку

[0; +∞ ),

обернена функція існує.

ПРИКЛАД:

Знайдіть функцію, обернену до функції

у = ¹/₆х – 7.

РОЗВ'ЯЗАННЯ:

у = ¹/₆х – 7,

6у = х – 42,

х = 6у + 42.

Оберненою буде функція

у = 6х + 42.

ПРИКЛАД:

Знайдіть функцію, обернену до функції

у = ¹/₃х + 2.

РОЗВ'ЯЗАННЯ:

у = ¹/₃х + 2,

3у = х + 6,

х = 3у – 6.

Оберненою буде функція

у = 3х – 6.

ПРИКЛАД:

Знайдіть функцію, обернену до функції
РОЗВ'ЯЗАННЯ:
Оберненою буде функція
ПРИКЛАД:

Знайдіть функцію, обернену до функції
РОЗВ'ЯЗАННЯ:
Оберненою буде функція
Графік зворотної функції.

ПРИКЛАД:

На малюнках зображені графіки функцій g і h.

Функція g обернена, оскільки немає такого значення функції, яке відповідало б різним значенням аргументу (будь-яка пряма, паралельна осі х, перетинає графік не більше ніж в одній точці).

Функція h не обернена, оскільки існує таке значення функції, наприклад у = 3, яке відповідає трьом різним значенням змінної х (пряма у = 3 перетинає графік в трьох точках).

Не для кожної функції існує обернена.

Графіки двох взаємно обернених функцій симетричні один до одного відносно бісектриси першого і третього координатних кутів, тобто відносно прямої

у = х.

Якщо точка (х; у) належить графіку функції у = f(х), то точка (у; х) належить графіку зворотної функції. Тому графік зворотної функції виходить із графіка функції у = f(х) за допомогою перетворення площини ху, що переводить точки (у; х) у точки (х; у). Цим перетворенням є перетворення осьової симетрії щодо прямої у = х (вісь симетрії).

Таким чином, щоб побудувати графік функції, зворотної до функції у = f(х), треба графік функції у = f(х) піддати перетворенню симетрії щодо прямої х = у.

ПРИКЛАД:

Якщо у = хⁿ, де х ≥ 0, n – натуральне, n ˃ 1, то
Помінявши х і у місцях, отримаємо
Графіки двох взаємно обернених функцій у = хⁿ і
симетричні щодо прямої у = х.
Завдання до уроку 16

Інші уроки:

Уроки математики и физики для школьников и родителей

вторник, 30 мая 2017 г.