Урок 12. Зростання і спадання функції

понедельник, 1 мая 2017 г.

Урок 12. Зростання і спадання функції

Функція називається зростаючою на даному проміжку, якщо для двох довільних значень аргументу з цього проміжку більшому значенню аргументу відповідає і більше значення функції.

Інакше: якщо при х₁ < х₂, де х₁ і х₂– довільні значення аргументу з даного проміжку, f(х₁) < f(х₂), то кажуть, що функція f(х) зростає на цьому проміжку.

Можна також говорити про зростання чи спадання функції не на всій області визначення, а тільки на окремих проміжках.

Функція називається спадаючою на даному проміжку, якщо для двох довільних значень аргументу з цього проміжку більшому значенню аргументу відповідає менше значення функції.

Якщо при х₁ < х₂, де х₁ і х₂– довільні значення аргументу з даного проміжку, f(х₁) > f(х₂), то кажуть, що на цьому проміжку функція f(х) спадає.

Іншими словами, функція зростає (зменшується) на проміжку, якщо які б два значення аргументу, що належать цьому проміжку, не взяти, виявиться, що більшому значенню аргументу відповідає більше (менше) значення функції.

Функції, що в якому-небудь проміжку тільки зростають або тільки спадають, називаються монотонними в цьому проміжку.

Якщо функція зростає в якому-небудь проміжку, то її графік із збільшенням х на цьому проміжку піднімається все вище, а якщо спадає, то її графік опускається всё нижче.

Іншими словами при русі вздовж осі абсцис зліва направо ордината графіка зростаючої функції збільшується,

а ордината графіка спадної функції зменшується.

Якщо функція зростає на всій області визначення, то її називають зростаючою функцією: якщо ж функція спадає на всій області визначення, то її називають спадною функцією.

ПРИКЛАД:

На рисунку зображено графік функції, областю визначення якої є проміжок

[–1; 4].

Ця функція є зростаючою, бо вона зростає на всій області визначення.

ПРИКЛАД:

На рисунку зображено графік функції, областю визначення якої є проміжок

[–1; 4].

Ця функція є спадною, бо вона спадає на всій області визначення.

Зростаючими, наприклад, є функції

у = 2х, у = √͞͞͞͞͞х,

а спадними – функції

у = –2х, у = –х.

ПРИКЛАД:

Розглянемо функцію y = f(x), графік якої зображено на рисунку.

На проміжку [–3; 2] графік <<іде в гору>>: якщо збільшувати значення х із цього проміжку, то відповідні значення функції збільшуватимуться. Наприклад, візьмемо значення аргументу

х₁ = –3 і х₂ = –1, тоді х₁ ˃ х₂. Оскільки

f(х₁) = f(–3) = –2, а

f(х₂) = f(–1) = 0,

то f(х₂) ˃ f(х₁).

Більшому значенню аргументу (х₂) відповідає більше значення функції (f(х₂)). Кажуть, що на проміжку [–3; 2] функція y = f(x) зростає (або є зростаючою). Такою ж вона є й на проміжку [5; 7]. на проміжку [2; 5] графік функції y = f(x) <<іде вниз>>: якщо збільшувати значення аргументу, то відповідні значення функції змешуватимуться. Кажуть, що на цьому проміжку функція y = f(x) спадає (або є спадною). Функція є ні зростаючою, ні спадною. Вона лише зростає або спадає на окремих проміжках.

Іноді кажуть і про не зростаючі і не спадні функції. Якщо при х₁ < х₂, де – х₁ і х₂ – довільні значення аргументу з даного проміжку, f(х₁) ≤ f(х₂), то функцію f(х) називають не спадною на цьому проміжку. Аналогічно визначається і не зростаюча функція. Кожна зростаюча функція є й не спадною, але не кожна не спадна є зростаючою.

Розглянемо для прикладу функцію у = [х], де символом [х] позначена ціла частина числа х, точніше, найбільше ціле число, яке не перевищує х.

ПРИКЛАД:

[2,4] = 2;

[0,25] = 0;

[7] = 7;

[ –3,2] = –4.

ПРИКЛАД:

Графік функції у = [х] наведено на рисунку.

Розглянемо цю функцію на проміжку

2 ≤ х < 3.

Як би не змінювалося значення х на цьому проміжку, значення функції залишається незмінним і дорівнює 2. Отже, дану функцію на цього проміжку можна назвати не спадною (і не зростаючою), але назвати її зростаючою або спадною на цьому проміжку не можна.

ПРИКЛАД:

Функція

у = х²

за будь-яких позитивних значеннях х зростає.

Справді, нехай

х₁ ˃ 0, х₂ ˃ 0 і х₂ ˃ х₁,

тоді
звідки
Це число позитивне, оскільки

х₂ – х₁ ˃ 0 і х₂ + х₁ ˃ 0.

Значить у₂ ˃ у₁, тобто функція у = х² зростає при позитивних значеннях х.

Та ж функція при будь-яких негативних значеннях х зменшується.
Справді, нехай

х₁ < 0, х₂ < 0 і х₂ ˃ х₁.

ТодіЦе число негативне, оскільки

х₂ – х₁ ˃ 0, а х₂ + х₁ < 0.

Значить у₂ < у₁тобто функція у = х² зменшується при негативних значеннях х.

ПРИКЛАД:

Функція

у = х³ + 2

зростає на всій області визначення, тобто при всіх дійсних значеннях х.

ПРИКЛАД:

Дослідити на монотонність функцію:

у = 2х³ + 3.

РОЗВ'ЯЗАННЯ:

Нехай х₁ < х₂. оді за властивостями числових нерівностей маємо

х³₁ < х³₂, 2х³₁ < 2х³₂,

2х³₁ + 3 < 2х³₂ + 3, тобто

f(х₁) < f(х₂).

Отже, х₁ < х₂, f(х₁) < f(х₂), а це означає, що функція

у = 2х³ + 3

зростає на всій числовій прямій.

ПРИКЛАД:

Побудуйте графік функції:

Користуючись побудованим графіком, знайдіть проміжки зростання і спадання функції.

РОЗВ'ЯЗАННЯ:

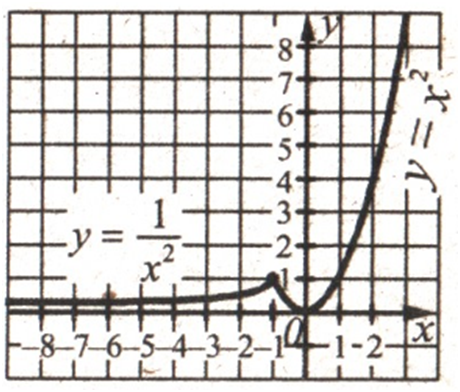
При х ≤ –1 графіком функції буде частина гіперболи
з проміжком зростання (–∞; –1].

При х ˃ –1 графіком функції буде частина параболи х² з проміжком спадання (–1; 0], зростання – [0; +∞).

ВІДПОВІДЬ; проміжки зростання: (–∞; –1] і [0; +∞), проміжки спадання: (–1; 0].

Завдання до уроку 12

Інші уроки:

Уроки математики и физики для школьников и родителей

понедельник, 1 мая 2017 г.