Розглянемо питання
графіку лінійної функції. При цьому ми припускатимемо, що область визначення
функції складається з усіх чисел
y = аx + b.
Це пряма, паралельна
прямий, що є графіком y
= аx, і проходить через
точку (0; b) на осі ординат.
Построить график функции:
у = –0,5х + 4.
РЕШЕНИЕ:
у = –0,5х + 4
y = аx + b
Якщо а = 0, графік лінійної функції буде пряма, паралельна до осі
абсцис, яка проходить через точку b на осі ординат. Лінійна функція, що задається
формулою y
= b, приймає те саме
значення при будь-якому х.
ПРИКЛАД:
Яка
з точок належить графіку функції ?
у
= 3 – 4х
А(0;
4), B(1; 3),
C(1; –1), D(3; 2).
РОЗВ'ЯЗАННЯ:
Графіку
функції у
= 3 – 4х належить точка С(1; –1),
бо
–1 = 3 – 4 ∙ 1,
ПРИКЛАД:
Укажіть
рівняння прямої, паралельної осі ординат.
х
+ у = 1,
х
– у = 1,
х
– 1 = 0,
у
+ 1 = 0.
РОЗВ'ЯЗАННЯ:
Паралельною
до осі ординат є пряма
х
– 1 = 0.
ПРИКЛАД:
у = ах + b, а = tg 120° =
–√͞͞͞͞͞3 ,
у = –√͞͞͞͞͞3х +b , 0 = –√͞͞͞͞͞3 ∙ 2 + b, b = 2√͞͞͞͞͞3,
у = –√͞͞͞͞͞3 x + 2√͞͞͞͞͞3 .
ПРИКЛАД:
Через
яку з точок проходить графік функції
у
= 0,8х + 4 ?
А(0;
4), B(1; 3),
C(5; 8), D(3; 2).
РОЗВ'ЯЗАННЯ:
Через
точку C(5; 8),
бо якщо х = 5, то
у
= 0,8 ∙ 5 + 4 = 8, 8 = 8.
ПРИКЛАД:
Знайдіть
точку перетину графіка функції
у
= 5х – 20
з
віссю ординат.
РОЗВ'ЯЗАННЯ:
х
= 0, у = 5 ∙ 0 – 20 = –20,
тому
точка перетину (0; –20).
ПРИКЛАД:
Через
яку точку проходить графік рівняння ?
у
= 3х – 4.
РОЗВ'ЯЗАННЯ:
Через
точку C(1; –1),
бо якщо х = 1, то
у
= 3 ∙
1 – 4 = –1, 8 = 8.
ПРИКЛАД:
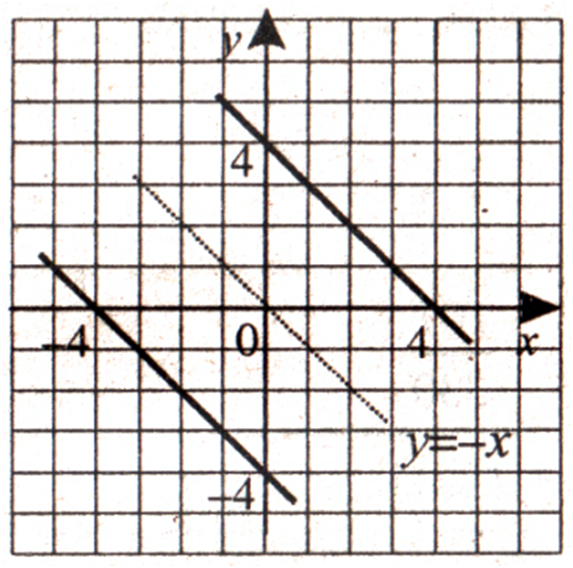
Побудуйте
графік функції:
|х + у|
= 4.
РОЗВ'ЯЗАННЯ:
Використавши
означення модуля, отримаємо:
1) якщо х + у ≥ 0, у ≥ –х,
то
х + у = 4, у = –х + 4
і
графіком цієї функції є пряма, яка проходить через точки (0; 4) і (4;
0).
2)
якщо х +
у < 0, у < –х, то
х + у = –4, у = –х – 4
Побудуйте
графік функції:
|х – у|
= 3.
РОЗВ'ЯЗАННЯ:
Використавши
означення модуля, отримаємо:
1) якщо х – у = 3, у = х
– 3.
Графіком
цієї функції є пряма, яка проходить через точки (0; –3) і (3;
0).
2)
якщо х –
у = –3, у = х + 3, то
ПРИКЛАД:
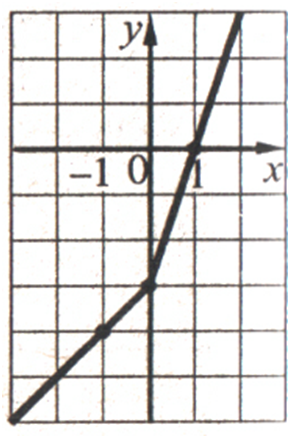
Побудуйте графік функції
РОЗВ'ЯЗАННЯ:Графік функції зображено на рисунку.Функція зростає на проміжку (–∞; +∞), проміжків спадання немає. зображено на рисунку.- Урок 1. Координатна площина
- Урок 2. Діаграми
- Урок 3. Графіки
- Урок 4. Множини
- Урок 5. Що таке функція ?
- Урок 6. Аналітичній спосіб задання функції
- Урок 7. Табличний спосіб задання функції
- Урок 8. Графічний спосіб задання функції
- Урок 9. Знаходження області визначення і області значення функції аналітичним способом
- Урок 10. Знаходження області визначення і області змині за допомогою графіка
- Урок 11. Нулі функції
- Урок 12. Зростання і спадання функції
- Урок 13. Екстремальні значення функцій
- Урок 14. Симетричні функції
- Урок 15. Парні і непарні функції
- Урок 16. Функція, зворотна даною
- Урок 17. Лінійна функція
- Урок 19. Пряма пропорційність
- Урок 20. Графік прямої пропорціональності
- Урок 21. Взаємне розташування графіків лінійних функцій
- Урок 22. Функція обернено пропорціональної залежності
- Урок 23. Графік функції обернено пропорціональної залежності
- Урок 24. Квадратична функція
- Урок 25. Графік функції у = aх2 + b
- Урок 26. Графік функції у = a(х - m)2 + n
- Урок 27. Графік функції у = aх2 + bx + c
- Урок 28. Функція у = √͞͞͞͞͞х і її графік
- Урок 29. Функція у = хn і її графік
- Урок 30. Побудова графіків функцій методом геометричних перетворень




















Комментариев нет:
Отправить комментарий