Кожен трикутник має три висоти. Висоти трикутника або їх продовження перетинаються в одній точці. У гострокутному трикутнику точка перетину висот розміщена всередині трикутника, у тупокутному – поза трикутником. Точка перетину висот або їх продовжень – ортоцентр.
Висоти трикутника, опущені на сторони а, b, с, позначаються відповідно через
ha, hb, hc
і обчисляються за формулами
– півпериметр трикутника.
ЗАДАЧА:
∠ AFE = 180° – ∠ EFD
= 76°,
тоді
∠ FAE = 90° – ∠ AFE
= 14°
(так як ∠ FEA
= 90°).
У
трикутнику ADC, кут D = 90°, отже
∠ С =
90° – ∠ FAE
= 90° – 14° = 76°.
ЗАДАЧА:
∠
FТС = 180° – ∠ СТВ = 28°,
тоді
∠
ТСF
= 90° – ∠ FТС = 62°
(так як ∠ ТEС
= 90°).
У
трикутнику AЕC, кут Е = 90°, отже
∠
А = 90° – ∠ ТСF
= 90° – 62° = 28°.
ЗАДАЧА:
У
трикутнику АВС:
∠ А =
60°, ∠ С =
80°,
СЕ
і
У
трикутнику AЕC, кут
Е = 90°,
∠ А =
60°,
тоді
∠
АСЕ
= 90° – 60° = 30°.
Аналогічно
у трикутнику АDС знаходимо, що
∠
DАС = 10°.
Так
як сума кутів трикутника дорівнює 180°, то
∠
АFС
= 180° – 10° – 30° = 140°.
Куті АFС
і ЕFD
рівні як вертикальні, тоді ∠ EFD = 140°.
ЗАДАЧА:
У
трикутнику ВОЕ, кут
Е = 90°,
∠ ОВЕ = 19°,
тоді
∠
ВОЕ
= 90° – 19° = 71°.
∠
FОЕ суміжний з ∠ ВОЕ , суміжний
з 180°
і,
отже,
∠
FОЕ = 109°.
Кожний трикутник має три бісектриси. Бісектриси трикутника перетинаються в одній точці, яка міститься усередині трикутника. Бісектриса внутрішнього кута трикутника поділяє протилежну сторону на відрізки, пропорційні до прилеглих сторін.
Бісектриса зовнішнього кута трикутника перетинає
продовження протилежної сторони в такій точці, відстань від якої до кінців цієї
сторони пропорціональні до прилеглих сторін.
У різностороннім трикутнику кожна бісектриса лежить
між медіаною і висотою, проведеними з цієї ж вершини.
Бісектриси трикутника перетинаються в одній точці. Точка
перетину бісектрис – інцентр.
У трикутнику АВС сторона ВС дорівнює 14 см, АC – 12 см. Знайти сторону АВ, якщо АD – бісектриса і DС дорівнює 8 см.
РОЗВ'ЯЗАННЯ:
– по властивості бісектриси трикутника.
ВD = ВС – DС =
ВІДПОВІДЬ: 9 см.
ЗАДАЧА:
У трикутнику АВС
∠ А = 60°, ∠ В = 80°.
Оскільки сума кутів трикутника дорівнює 180°, тому ∠ С дорівнюватиме:
∠ С
= 180° – 80°
– 60° = 40°.
Бісектриса ділить ∠ ВАС навпіл,
отже ∠ DАС дорівнює 30°.
Тоді ∠ АDС дорівнюватиме 110°.
ВІДПОВІДЬ:
∠ С
= 40°,
∠ DАС = 30°,
∠ АDС = 110°.
ЗАДАЧА:
Відрізок АМ – бісектриса трикутника АВС,
АВ = 30 см,
АС
= 40 см,
СМ – ВМ =
5
см.
Знайдіть ВС.
РОЗВ'ЯЗАННЯ:
ВМ = х, СМ = х + 5.
ВС
= х + х + 5 = 35 (см).
ЗАДАЧА:
∠
АКР = ∠
РКQ, тому що вони вертикальні.
∠
КАВ = 0,5 ∙ ∠
САВ,
∠
АВК = 0,5 ∙ ∠
АВС,
тоді з урахуванням того, що сума кутів у трикутнику дорівнює 180°
(∠
САВ + ∠
АВС + ∠
С = 180°).
∠
КАВ + ∠
АВК =
=
0,5∙ (∠ САВ + ∠
АВС)
=
= 0,5∙ (180° – 75°)
= 52,5°, значить,
∠
АКВ = 180°
– (∠
КАВ + ∠
АВК)
=
= 180° – 52,5° = 127,5°.
Таким чином,
Медіаною трикутника називають відрізок, який сполучає вершину
трикутника із серединою протилежної сторони.
Кожен трикутник має три медіани.
Медіани будь-якого трикутника перетинаються в одній
точці, яка знаходиться в середині трикутника і називається центроїдом (центр
мас або центр тяжіння).
Медіану позначають буквою m..
О –
центроїд трикутника АВС.
AO
: ON = BO : OL =
=
CO : OM = 2 : 1
Якщо медіани проведені до сторін a,
b і c, відповідно
записують так: ma mb і mc.
ВС = а, АС = b, АВ = с, то:
Медіана трикутника є
геометричним місцем точок, що є серединами відрізків прямих, укладених
усередині трикутника, паралельних тій стороні, до якої проведена медіана.
ЗАДАЧА:
AM =
MN,
MN =
NC,
тоді
AC =
AM + MN + NC = 3MN,
AC = AM :
MN = 3.
ЗАДАЧА:
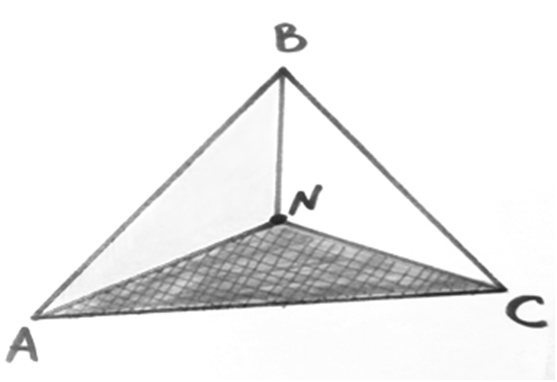
У трикутнику АВС задані медіани
ma, mb, mc.
Знайти
сторони трикутника.
РОЗВ'ЯЗАННЯ:
Позначимо
сторони трикутника
АВ = с, АС = b, ВС = а.
- Урок 1. Точка і пряма
- Урок 2. Кут
- Урок 3. Паралельні і перпендикулярні прямі
- Урок 4. Коло
- Урок 5. Кут і коло
- Урок 6. Трикутник (1)
- Урок 8. Прямокутній трикутник (1)
- Урок 9. Прямокутній трикутник (2)
- Урок 10. Рівнобедрений (рівносторонній) трикутник (1)
- Урок 11. Рівнобедрений (рівносторонній) трикутник (2)
- Урок 12. Периметр трикутника.
- Урок 13. Периметр рівнобедреного трикутника
- Урок 14. Трикутник і коло
- Урок 15. Прямокутний трикутник і коло
- Урок 16. Рівнобедрений трикутник і коло
- Урок 17. Чотирикутники
- Урок 18. Паралелограм
- Урок 19. Периметр паралелограма
- Урок 20. Прямокутник
- Урок 21. Периметр прямокутника
- Урок 22. Квадрат
- Урок 23. Ромб
- Урок 24. Периметр ромба
- Урок 25. Трапеція
- Урок 26. Рівнобічна трапеція
- Урок 27. Периметр трапеції
- Урок 28. Чотирикутник і коло (1)
- Урок 29. Чотирикутник і коло (2)
- Урок 30. Многокутник
- Урок 31. Правильний многокутник
- Урок 32. Осьова і центральна симетрії



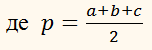




























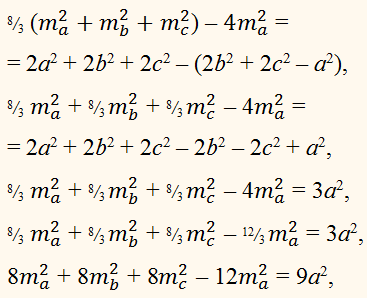




Комментариев нет:
Отправить комментарий