Урок 4. Коло

понедельник, 25 августа 2014 г.

Урок 4. Коло

ВІДЕОУРОК

Довжина кола.

Візьмемо круглу склянку, поставимо на аркуш паперу й обведемо її олівцем.

На папері вийде коло.

Якщо ми візьмемо циркуль і встановимо нерухомо одну його ніжку (з гострим кінцем) у крапку, а іншу (з олівцем) обертатимемо по площині навколо нерухомої точки, не змінюючи розчину циркуля, то олівець опише замкнуту криву лінію, всі точки якої будуть перебувати на однаковій відстані від зазначеної нерухомої точки. Ми отримаємо криву лінію, яка називається коло.

Коло – геометрична фігура, що складається з усіх точок, розташованих на заданій відстані від цієї точки – центру кола.

Внутрішня область кола називається кругом. Кордон круга його коло.

Іншими словами, коло - це контур кола (те, що ми малюємо циркулю). Коло – та частина аркуша паперу, що залишається всередині.

Крапка, залишена циркулем гострим кінцем, називається центром кола. Відстань від центру до будь-якої точки кола називається її радіусом. З побудови слід, що це радіуси одного кола рівні між собою. Відрізок прямої лінії, що з'єднує дві будь-які точки кола і проходить через її центр, називається діаметром. Діаметр дорівнює двом радіусам. Отже, всі діаметри одного кола рівні між собою. Діаметр кола зазвичай позначають буквою d або D. Діаметр дорівнює двом радіусам:

d = 2r, D = 2R.

Якщо опоясати склянку ниткою, а потім розрівняти її, то довжина нитки буде наближено дорівнювати довжині намальованого кола.

Чим більший діаметр кола, тим більша його довжина. Для всіх кіл відношення довжини кола до довжини його діаметра є одним і тим самим числом. Це число позначають грецькою буквою π.

Якщо позначити довжину кола буквою С, а довжину діаметра буквою d, то довжину кола обчислюють за формулою:

C = πd.

Оскільки діаметр кола вдвоє більший за його радіус, то довжина кола з радіусом r дорівнює 2πr. Дістали другу формулу для довжини кола:

C = 2πr,

Тобто, щоб знайти довжину кола, треба його діаметр помножити на π, або два радіуси помножити на π.

Підрахунки показали, що з точністю до десятитисячних π ≈ 3,1415… . Якщо значення числа π округлити до сотих, то дістанемо значення 3,14. Приблизно таку саму точність дає значення π ≈ ²²/₇.

ЗАДАЧА:

Визначити радіус кола, якщо вона довша за свій діаметр на 107 см.

РОЗВ'ЯЗАННЯ:

Позначимо довжину кола як С, а діаметр як D. Таким чином

С – D = 107.

Довжина кола дорівнює

C = πD,

тому
Звідки радіус кола
Дуга кола.

Дуга кола – кожна з двох частин кола, на які коло ділиться двома точками.
∪ АВ – дуга кола.

Півколо – дуга, кінці якої є кінцями діаметра кола.

∪ СТ – півкола, тому що відрізок СТ – діаметр.

Дуги кола вимірюються в градусах.

Відрізок прямої лінії, що з'єднує дві будь-які точки кола і не проходить через її центр, називається хордою кола.

Діаметр кола, який проходить через середину хорді, перпендикулярний до неї. Діаметр, перпендикулярний до хорді, ділити її і дугу, яку вона стягує, навпіл. Справедливо й обернене твердження: якщо діаметр кола проходити через середину хорді, яка не є діаметром, чи через середину дуги, яку вона стягує, то цей діаметр перпендикулярний до даної хорди. Рівні дуги стягуються рівними хордами, а рівні хорди стягують рівні дуги. Дуги, які лежать між паралельними хордами, рівні.

Взаємне розташування прямої та кола.

Відомі три випадки взаємного розміщення прямої та кола, якщо це пряме та коло лежать в одній площині:

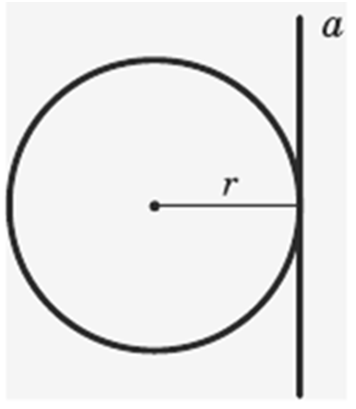
– пряма та коло не мають спільних точок;

– пряма та коло мають одну спільну точку;

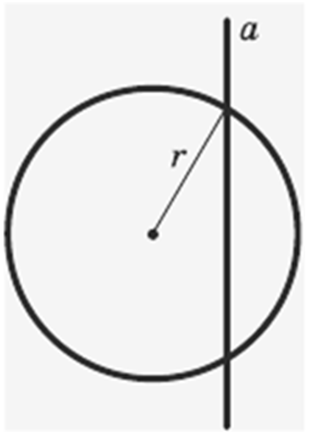
– пряма та коло мають дві спільні точки.

Перерахуємо умови, що визначають всі можливі випадки взаємного розташування прямої та кола, залежно від відстані між центром кола та прямою.

– якщо відстань від центру кола до деякої прямої більше радіусу, то ця пряма не має з колом загальних точок, при цьому коло лежить по одну сторону від прямої;
– якщо відстань від центру кола до прямої дорівнює радіусу, то коло має з прямою єдину загальну точку, тобто пряма стосується кола і в цьому випадку коло лежить по один бік від прямої.
Пряму, яка має з колом лише одну спільну точку, називають причетною до колу. При цьому дана точка кола називається точкою дотику. Дотикова до кола не має з ним інших спільних точок, крім точки дотику.

Справедливо таке:

– дотична до кола перпендикулярна до радіусу, проведеного в точку торкання;

– якщо пряма перпендикулярна радіусу кола і проходить через його кінець, що лежить на колі, то вона є дотичною до цього кола

– якщо з даної точки провести дві дотичні до кола, то відрізки дотичних, які з'єднують цю точку з точками дотику, дорівнюють.

Всі точки дотичної, крім точки дотику, лежать поза цим колом. Дійсно, якщо припустити, що на дотичній є хоча б одна точка, що лежить усередині кола, то пряма повинна перетинати коло у двох точках, тому вона не може бути дотичною.

Пряме і коло можуть мати тільки одну загальну точку, але через цю точку може проходити безліч прямих, що не лежать з колом в одній площині.

– якщо відстань від центру кола до деякої прямої менша за радіус, то ця пряма має з колом дві спільні точки, тобто пряма перетинає коло і розбиває коло на дві частини, пряму, яка перетинає коло у двох точках, називають січною;
Якщо пряма проходить через точку, внутрішню щодо кола, то вона є січною, тобто перетинає коло у двох точках.

ЗАДАЧА:

Скільки спільних точок має пряма і коло, діаметр якого дорівнює 8 см, якщо пряма розміщена на відстані 5 см від центра кола ?

РОЗВ'ЯЗАННЯ:

Оскільки діаметр кола дорівнює 8 см, то радіус дорівнює 4 см. Відстань від центра кола до прямої – 5 см, тому коло й пряма не перетинаються.
Розташування кіл.

Два кола можуть бути розміщені так:

– кола не мають спільних точок.

Вони лежать або: одне поза кругом іншого, у цьому випадку відстань між центрами буде більша від суми радіусів або одне всередині круга іншого, у цьому випадку відстань між центрами буде меншою від різниці радіусів.

– кола мають одну спільну точку.

Кола, які мають одну спільну точку, називають дотичними. Спільну точку називають точкою дотику. Говорять, що два кола, які мають спільну точку, дотикаються в цій точці, якщо вони мають в ній спільну дотичну.

Дотик кіл називається внутрішнім, якщо центри кіл лежать по один бік від їх спільної дотичної.
Дотик кіл називається зовнішнім, якщо центри кіл лежать по різні боки від їх спільної дотичної.
ЗАДАЧА:

Два кола діаметром 4 см і 8 см стосуються зовнішнім чином. Чому дорівнює відстань між центрами кіл ?

РОЗВ'ЯЗАННЯ:

Радіуси кіл ОА і О₁А перпендикулярні їх загальної дотичної, що проходить через точку А.
Тому

ОО₁ = ОА + О₁А = 6 см.

ЗАДАЧА:

Два кола дотикаються зовні. Знайти довжину їхньої спільної зовнішньої дотичної, якщо радіуси кіл рівна 16 см і 25 см.

РОЗВ'ЯЗАННЯ:

O₁D₁ ⊥ OD₁, O₂D₂ ⊥ OD₁.

Побудуємо точку Е на O₂D₂, так що O₁E D₂D₁– прямокутник, тоді

O₂E = R₂ – R₁ = 9 (см),

O₁O₂ = R₂ + R₁ = 41 (см).

∆ O₁O₂E: (∠ E = 90°),

ВІДПОВІДЬ: 40 см

ЗАДАЧА:

Яке взаємно розміщення двох кіл з діаметрами 10 см і 20 см, якщо відстань між їхніми центрами дорівнює 15 см ?

РОЗВ'ЯЗАННЯ:
Кола дотикаються.

– кола мають дві спільні точки, у цьому випадку відстань між центрами буде меншою від суми їх радіусів, але більшою від їх різниці.

Пряму, яка проходить через центри двох кіл, називають лінією центрів.

Два кола, що знаходяться в одній площині і мають загальний центр, називаються концентричними колами.

Коло – геометричне місце точок, рівновіддалених від цієї точки.

Коло радіусу r – геометричне місце точок, відстань від яких до цієї точки не перевищує r.

Якщо хорди АВ і СD кола перетинаються в точці S, то

АS × ВS = СS × DS.

Якщо з точки Р до кола проведено дві січні, що перетинають коло відповідно в точках А, В і С, D, то

АР × ВР = СР × DР.

ПРИКЛАД:

На яке найбільше різних частин, які мають спільних точок, крім своїх кордонів, можуть розбивати площину:

а) два кола;

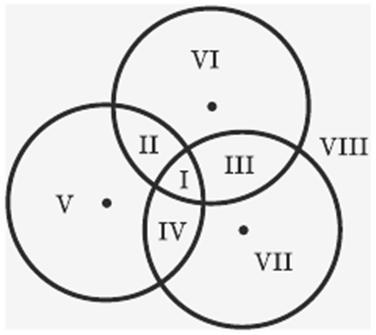
б) три кола ?

РОЗВ'ЯЗАННЯ:

Зобразимо на малюнку відповідні умови випадки взаємного розташування фігур. Запишемо відповідь:

а) чотири частини,
б) вісім частин.
Завдання до уроку 4

Інші уроки:

Уроки математики и физики для школьников и родителей

понедельник, 25 августа 2014 г.