Урок 6. Трикутник (1)

суббота, 20 сентября 2014 г.

Урок 6. Трикутник (1)

ВІДЕОУРОК
Трикутником називають геометричну фігуру, яка складається із трьох точок, що не лежать на одній прямій, трьох відрізків, які сполучають ці точки, й обмеженої ними частини площини.

Точки А, В і С називають вершинами, а відрізки

АВ, ВС, АС – сторонами трикутника.

Трикутник називають і позначають за його вершинами. Трикутник, зображений на рисунку, позначають так ∆ АВС (читають: трикутник АВС), або ∆ ВСА, або ∆ АСВ. Кути АВС, ВАС, АСВ – кути трикутника АВС. Їх можна позначити й однією буквою: ∟В, ∟А, ∟С. Сторони трикутника АВС можна позначати маленькими буквами a, b і c. При цьому дотримуються такого порядку: проти кута А лежить сторона а або ВС; проти кута В лежить сторона b або АС; проти кута С лежить сторона с або АВ. Кут В називають кутом, протилежним до сторони АС, а кути А і С – прилеглими до цієї сторони.

Побудова трикутників.

ЗАДАЧА:

Побудуйте трикутник АВС, у якому

АВ = 5 см,

ВС = 4 см,

∠ В = 40°.

РОЗВ'ЯЗАННЯ:

Накреслимо промінь ВМ. За допомогою транспортира відкладемо од цього променя кут МВN, градусна міра якого 40°.

Від вершини В на стороні ВM цього кута відкладемо відрізок ВА завдовжки 5 см, а на стороні ВN – відрізок ВС завдовжки 4 см. Сполучивши точки А і С відрізком, дістанемо шуканий трикутник АВС.

ЗАДАЧА:

Побудуйте трикутник АВС, у якому

АВ = 6 см,

∠ А = 60°,

∠ В = 20°.

РОЗВ'ЯЗАННЯ:

Накреслимо відрізок АВ завдовжки 6 см.
За допомогою транспортира будемо з одного боку від прямій АВ кут ВАN, що дорівнює 60°, і кут АВК, що дорівнює 20°. Точка перетину променів АN і ВК і буде третьою вершиною С шуканого трикутника АВС.

ЗАДАЧА:

Побудуйте трикутник АВС, у якому

АВ = 3,5 см,

АС = 3 см,

ВС = 4 см.

РОЗВ'ЯЗАННЯ:

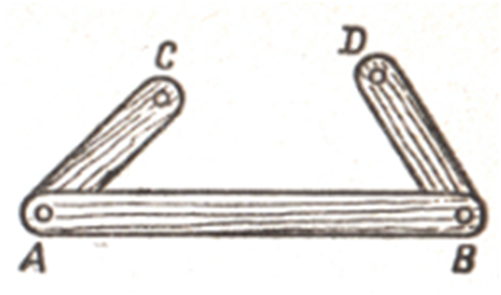
Накреслимо відрізок АВ завдовжки 3,5 см. Вершина С буде віддалена від точки А на 4 см, тому вона має лежати на колі з центром А і радіусом 4 см.
Вершина С має бути віддалена од точки В на 3 см, тому вона повинна лежати на колі з центром В і радіусом 3 см. Побудуємо ці два кола. Одну з точок перетину позначимо С і сполучимо її з точками А і В.
Якщо з’єднати три рейки так, як на малюнку,

то, не розтягуючи, не стискаючи і не згинаючи рейок, не можна змінити форми трикутника. Кажуть, що трикутник – жорстка фігура. Цією властивістю трикутника користуються на практиці.

Довжини відрізків, за якими будують трикутник, не можна задавати довільно. Сума довжин коротких рейок на малюнку

менша від довжини більшої рейки. Тому, якщо обертати короткі рейки навколо точок А і В, їх кінці С і D ніколи не сумістяться і трикутника не вийде.

Трикутник можна побудувати за трьома сторонами, якщо довжина більшої сторони менша за суму довжин двох інших сторін

ПРИМЕР:

Чи існує трикутник АВС зі сторонами:

АВ = 5 см,

АС = 18 см,

ВС = 7 см.

РОЗВ'ЯЗАННЯ:

АС найбільша сторона, що дорівнює 18 см. Сума двох інших сторін дорівнює 12 см, вона менша за довжину більшої сторони, отже трикутник побудувати не можна.

ПРИМЕР:

Чи існує трикутник АВС зі сторонами:

АВ = 7 см,

АС = 8 см,

ВС = 12 см.

РОЗВ'ЯЗАННЯ:

ВС найбільша сторона, що дорівнює 12 см. Сума двох інших сторін дорівнює 15 см, вона більша за довжину більшої сторони, отже трикутник побудувати можна

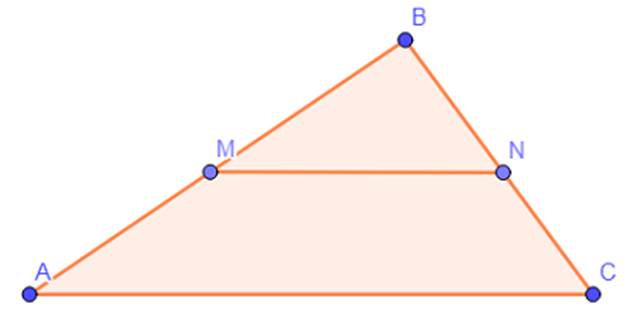
Середня лінія – пряма, що з'єднує середини двох сторін.

Наприклад: у трикутнику АВС відрізок МN – середня лінія

Трикутник має три середні лінії. При проведенні всіх трьох середніх ліній утворюються 4 рівні трикутники.

Властивості сторін і кутів.

Будь – яка сторона трикутника менша від суми двох інших його сторін і більша за їх різницю:

c – b < a < c + b, b < c.

Щоб перевірити, чи можна з трьох відрізків а, b і с утворити трикутник, досить перевірити, чи буде найдовший з цих відрізків меншим від суми двох інших.

ЗАДАЧА:

У трикутнику АВС відомо, що АВ = 5 см, ВС = 10 см. Якій із наведених величин може дорівнювати довжина сторони АВ ?

4 см, 5 см, 8 см, 17 см.

РОЗВ'ЯЗАННЯ:

АВ – ВС < АС < АВ + ВС,

10 – 5 < АС < 10 + 5,

5 < АС < 15.

Отже, АС = 8 см.

Сума кутів трикутника дорівнює 180°.

Проти більшої сторони трикутника лежить і більший кут:

якщо b > а, то β > α; і навпаки,

якщо β > α, то b > а; а також,

якщо а = b, то α = β.
ЗАДАЧА:

У трикутнику АВС:

∠ А = 30°, ∠ В = 45°.

Яка сторона трикутника є найбільшою ?

РОЗВ'ЯЗАННЯ:

Знайдемо кут С.

∠ С = 180° – (30° + 45°) = 105°.

∠ С – найбільший, тому найбільшою стороною є АВ.

Зовнішнім кутом трикутника (∠ КВС) називають кут, одержаний стороною трикутника та продовженням його іншої сторони.

При кожній вершині є два зовнішні кути. Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів трикутника, не суміжних із ним.

∠ КВС = ∠ АСВ + ∠ САВ.

Зовнішній кут трикутника більший від кожного внутрішнього кута, не суміжного з ним. Якщо кожна з двох фігур (трикутників) дорівнює третій, то перша та друга фігура (трикутник) теж рівні.

Сума зовнішніх кутів трикутника, взятих по одному при кожній вершині, дорівнює 360°.

∠ 1 + ∠ 2 + ∠ 3 = 360°.

Трикутник, у якого всі сторони різні, називається різнобічним.

Трикутник розбиває площину на дві області: внутрішню та зовнішню. Фігура, що складається з трикутника та його внутрішньої області, також називається трикутником. Кутами трикутника АВС називають кути ВАС, АВС та АСВ. Їх позначають так:

∠ А, ∠ В, ∠ С.

Кожен трикутник має три кути.

Якщо трикутник має тупий кут, його називають тупокутним трикутником. Трикутник, у якого всі кути гострі, називається гострокутним. Трикутник не може мати двох прямих або двох тупих кутів. У кожного трикутника зазвичай два кути – гострі. Якщо один з кутів – тупий, то два інші кути – гострі. У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона.

Два трикутники називаються рівними, якщо при накладенні один на одного вони поєднуються.

При позначенні вершин рівних трикутників має значення порядок запису літер: літери, які відповідають рівним кутам, необхідно записувати в обох трикутниках на однакових місцях.

У рівних трикутниках проти рівних сторін лежать рівні кути, а проти рівних кутів – рівні сторони.

Загальні ознаки рівності трикутників.

– якщо дві сторони та кут між ними одного трикутника рівні відповідно двом сторонам та куту між ними іншого трикутника, то такі трикутники рівні;

– якщо сторона та прилеглі до неї кути одного трикутника рівні відповідно до сторони та прилеглих до неї кутів іншого трикутника, то такі трикутники рівні;

– якщо три сторони одного трикутника рівні відповідно до трьох сторін іншого трикутника, то такі трикутники рівні.

ЗАДАЧА:

Виміряти відстань між двома точками на місцевості, між якими є перешкода (не можна пройти безпосередньо та виміряти).

РОЗВ'ЯЗАННЯ:

Припустимо, що між точками А і В знаходиться озеро. Виміряємо відстань між ними.
Виберемо точку С, від якої можна пройти прямою до обох точок А і В. Вийшов трикутник АСВ.

Якщо побудувати йому рівний трикутник, де є доступ до всіх трьох сторін, то завдання буде вирішено.

Продовжимо сторону АС та відкладемо на ній відрізок СD = АС. Аналогічно збудуємо відрізок СЕ = ВС.
Отриманий трикутник DСЕ дорівнює трикутнику АСВ, тому що кути ∠ ЕСD, ∠ АСВ рівні, як вертикальні, а сторони

СD = АС, СЕ = ВС

за побудовою.

Співвідношення між елементами довільного трикутника.

Квадрат сторони, що лежить проти гострого кута, дорівнює сумі квадратів двох інших сторін без подвоєного добутку однієї з цих сторін і проекції на неї другої сторони.

c² = a² + b² – 2ab_a
= a² + b² – 2ba_b.

Квадрат сторони, що лежить проти тупого кута, дорівнює сумі квадратів двох інших сторін, додатній до подвоєного добутку однієї з цих сторін і проекції її на продовження другої сторони.

c² = a² + b² + 2ab_a
= a² + b² + 2ba_b.

Завдання до уроку 6

Інші уроки:

Уроки математики и физики для школьников и родителей

суббота, 20 сентября 2014 г.