Урок 20. Прямокутник

воскресенье, 30 ноября 2014 г.

Урок 20. Прямокутник

ВІДЕОУРОК

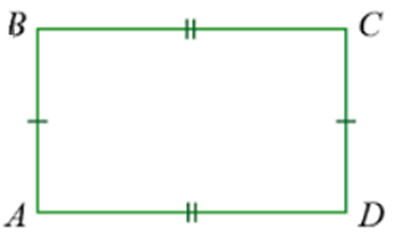
Серед чотирикутників особливе місце посідає прямокутник.

Прямокутник – паралелограм, який має всі кути прямі, а діагоналі рівні.

ABCD – прямокутник.

∠ A = ∠ B = ∠ C = ∠ D = 90°.

Прямокутник разом із частиною площини, яку він обмежує, називається плоским прямокутником. У нього 4 вершини, 4 сторони та 4 кути. Усі кути прямокутника – прямі, протилежні сторони – попарно рівні, але суміжні сторони (довжина та ширина) мають різні довжини. Прямокутник – окремий вид паралелограма, тому має всі властивості паралелограма. У прямокутника:

– протилежні стороні рівні;
– протилежні кути рівні;
– діагональ діліть його на два рівні трикутники;
– діагоналі точкою перетину діляться навпіл;
– діагоналі прямокутника рівні;
– сума кутів, прилеглих до однієї сторони, дорівнює 180°.

Якщо діагоналі в паралелограмі рівні, цей паралелограм – прямокутник.

Побудувати прямокутник можна так.

Побудуємо прямокутник АВСD, у якого

АD = 6 см,

АВ = 4 см.

Накреслимо пряму ЕF і відкладемо на ній відрізок АD завдовжки 6 см.

За допомогою косинця побудуємо з одного боку від прямої ЕF прямі кути NАF і МDF. Відкладемо на промені АN відрізок АВ завдовжки 4 см і на промені DМ – відрізок DС, що дорівнює 4 см. Сполучивши точки В і С відрізком, дістанемо шуканий прямокутник АВСD.

ЗАДАЧА:

Яку частину прямокутника затушоване на рисунку ?

РОЗВ'ЯЗАННЯ:

Затушовані 2 з 6 однакових прямокутників, тобто

²/₆ = ¹/₃ частина.

ЗАДАЧА:

О – точка перетину діагоналей прямокутника АВСD,

∠ СОD = 52°.
Знайдіть ∠ DВС.

РОЗВ'ЯЗАННЯ:

∠ ОВС =∠ ОСВ,

∠ СОD = ∠ ОВС +∠ ОСВ =

= 2∠ ОВС,

∠ DВС =∠ ОВС =

= ∠ СОD : 2 =

= 52° : 2 = 26°.

ЗАДАЧА:

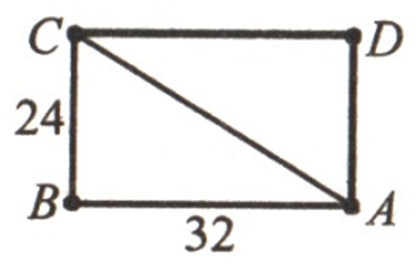
Сторони прямокутника дорівнюють 32 см і 24 см. Знайдіть довжину діагоналі прямокутника.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.

За теоремою Піфагора
ЗАДАЧА:

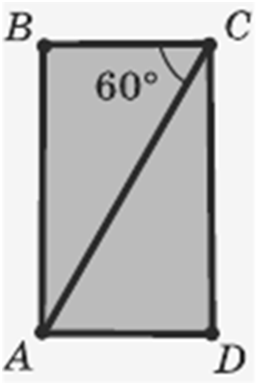
Сторона прямокутника дорівнює 4 см і утворює із діагоналлю кут 60°. Знайдіть цю діагональ.

РОЗВ'ЯЗАННЯ:

З умови завдання маємо:

АВСD – прямокутник,

ВС = 4 см,

∠ ВСА = 60°.

Знайдіть АС.

∆ АВС – прямокутний, у ньому катет

ВС = 4 см, а

∠ ВАС = 30°.

За властивістю катета, що лежить у прямокутному трикутнику проти кута 30°,

ВС = 0,5АС.

Значить АС = 8 см.

ЗАДАЧА:

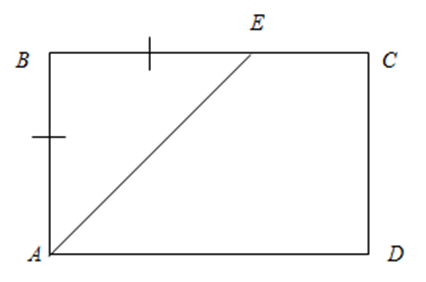
Дано: АВСD – прямокутник, АВ = ВЕ.

Знайти: ∠ ВАЕ.
РОЗВ'ЯЗАННЯ:

В ∆ АВЕ ∠ В = 90° (як один з кутів прямокутника).

АВ = ВЕ,

отже ∆ АВЕ – рівнобедрений з основою АЕ.

∠ А = ∠ Е

як кути при основі рівнобедреного трикутника, в сумі вони мають 90° як гострі кути прямокутного трикутника. Значить,

∠ А = ∠ Е = 45°,

∠ ВАЕ = 45°.

ВІДПОВІДЬ: 45°

ЗАДАЧА:

Діагональ ділить кут прямокутника у відношенні 1 : 2, а менша сторона дорівнює 12 см. Знайдіть діагональ прямокутника.

РОЗВ'ЯЗАННЯ:

Нехай ЕКРМ – даний прямокутник у якого

∠ РЕК : ∠ РЕМ = 2 : 1.

∠ КЕМ = 90° (як кут прямокутника).

Позначимо через k коефіцієнт пропорційності, тоді

∠ РЕК = 2k, а ∠ РЕМ = k.

Отже,

2k + k = 90°.

Звідки

∠ РЕК = 60°, а ∠ РЕМ = 30°.

Розглянемо

∆ РЕМ (∠ М = 90°).

РМ = ¹/₂ЕР (як катет протилежний куту в 30°).

Значить

ЕР = 2РМ = 24 см.

ВІДПОВІДЬ: 24 см.

ЗАДАЧА:

У рівнобедрений прямокутний трикутник вписано прямокутник так, що дві його вершини знаходяться на гіпотенузі, а дві інші – на катетах. Чому рівні сторони прямокутника, якщо відомо, що вони відносяться як 5 : 2, а гіпотенуза трикутника дорівнює 45 см ?

РОЗВ'ЯЗАННЯ:

∆ АВС – рівнобедрений, звідси

∠ А = ∠ С = ¹/₂ (180° – 90°) = 45°.

∆ АFК и ∆ СEL – рівнобедрені, тому що

∠ АКF = 180° – ∠ F – ∠ А =

= 180° – 90° – 45⁰ = ∠ А

і аналогічно ∠ ЕLК = ∠ С.

Тому АF = FК и LE = ЕС.

До того ж КF = LE (сторони прямокутника), так що

АF = КF = LЕ = ЕС.

Нехай FК = 2х, а КL = 5х.

Тоді АF = ЕС = FК = 2х

і FЕ = КL = 5х.

Отримаємо

АС = АF + FЕ + EС =

= 2х + 5х + 2х = 9х = 45,

звідки х = 5.

Далі,

FК = 2х = 10 см,

КL = 5х = 25 см.

ВІДПОВІДЬ: 10 см, 25 см.

ЗАДАЧА:

Бісектриса кута А прямокутника АВСD діліть його сторону ВС на відрізки ВМ і МС завдовжки 10 см і 14 см відповідно. На відрізки якої довжини ця бісектриса ділить діагональ прямокутника ?

РОЗВ'ЯЗАННЯ:

Нехай АВСD – заданий прямокутник,
АМ – бісектриса кута А,

ВМ = 10 см,

МС = 14 см.

Тоді ВС = 24 см.

Оскільки АМ – бісектриса кута, то

∠ 1 = ∠2.

∠ 1 = ∠ 3

як внутрішні різносторонні для паралельних прямих ВС і АD та січної АМ.

Одержимо: ∠ 2 = ∠ 3.

Отже, трикутник АВМ – рівнобедрений,

АВ = ВМ = 10 см.

З ∆ ВАD (∠ А = 90°):

О – точка перетину бісектриси АМ і діагоналі ВD.

Нехай ВО = х, тоді

ОD = 26 – х.

За властивістю бісектриси АС ∆ АВD:

12х = 130 – 5х,

17х = 130, х = ¹³⁰/₁₇.

Отже,

ВО = ¹³⁰/₁₇ = 7¹¹/₁₇ (см).

ОD = 26 – 7¹¹/₁₇ = 18⁶/₁₇ (см)

ВІДПОВІДЬ:

7¹¹/₁₇ см, 18⁶/₁₇ см

ЗАДАЧА:

Бісектриса кута прямокутника діліть діагональ на відрізки завдовжки 30 см і 40 см. На відрізки якої довжини ділить ця бісектриса сторону прямокутника ?

РОЗВ'ЯЗАННЯ:

Нехай АВСD – заданий прямокутник,
АМ – бісектриса кута А, яка перетинає діагональ ВD у точці О,

ВО = 30 см,

ОD = 40 см.

Тоді ВD = 30 + 40 (см).

Оскільки АМ – бісектриса кута, то

∠ 1 = ∠2,

∠ 1 = ∠ 3

як внутрішні різносторонні для паралельних прямих ВС і АD та січної АМ.

Одержимо:

∠ 2 = ∠ 3.

Отже, трикутник АВМ – рівнобедрений,

АВ = ВМ.

За властивістю бісектриси кута А у трикутнику ВАD одержимо:

Звідси

АВ = 3х, АD = 4х.

З ∆ ВАD (∠ А = 90°):

АВ² + АD² = ВD²,

9х² + 16х² = 4900,

25х² = 4900, х = 14.

Отже,

АВ = 3 ∙ 14 = 42 (см).

АD = 4 ∙ 14 = 56 (см).

Оскільки

АВ = ВМ, то

ВМ = 42 см,

МС = ВС – ВМ =

= 56 – 42 = 14 (см).

ВІДПОВІДЬ: 42 см, 14 см

Завдання до уроку 20

Інші уроки:

Уроки математики и физики для школьников и родителей

воскресенье, 30 ноября 2014 г.