Урок 17. Чотирикутник

пятница, 28 ноября 2014 г.

Урок 17. Чотирикутник

ВІДЕОУРОК
Чотирикутником називають фігуру, яка складається з чотирьох точок, жодні три з яких не лежать на одній прямій, та чотирьох відрізків, які послідовно з’єднують ці точки.

На малюнку точки А, В та С лежать на одній прямій, значить це не чотирикутник.

На малюнку прямі АD і ВС перетинаються, це не чотирикутник.

Дані точки називаються вершинами чотирикутника, а відрізки, що їх сполучають, – сторонами чотирикутника. Чотирикутник позначають послідовно записуючи його вершини. Наприклад, чотирикутник, зображений на рисунку, можна позначити так:

ABCD, BCDA, CDAB, DABC.

але не можна позначати ABDС (B і D – несусідні вершини).

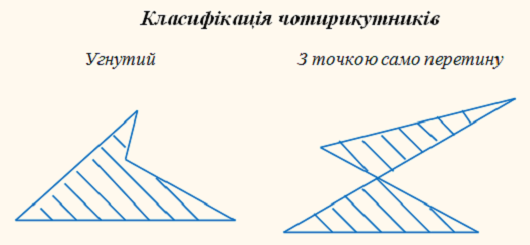
Чотирикутники бувають опуклі й не опуклі.

Чотирикутник називають опуклим, якщо він лежить з одного боку від кожної прямої, яка містить його сторону.

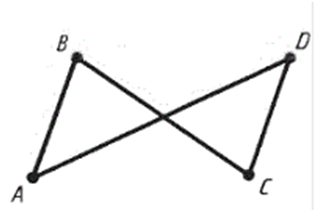
Один із кутів чотирикутника може бути більшим від розгорнутого. Такий чотирикутник не опуклий.

На рисунку A, B, C і D – вершини чотирикутника,

AB, BC, CD і DA – сторони чотирикутника, кути DAB, ABC, BCD і CDA – кути чотирикутника. Кути позначають і так:

∠ A, ∠ B, ∠ C, ∠ D відповідно.

Відрізки, що сполучають протилежні вершини чотирикутника, називаються діагоналями.

Кожний чотирикутник має дві діагоналі. Діагоналі чотирикутника перетинаються. Кожна діагональ розбиває чотирикутник на два трикутника.

Сторони чотирикутника, що виходять з однієї вершини, називаються сусідніми сторонами.

Сторони, які не мають спільного кінця, називаються протилежними сторонами.

Протилежні вершини чотирикутника – вершини, які не з'єднані спільною стороною.

Кожна сторона чотирикутника менша за суму трьох інших сторін. Щоб установити, чи можна з чотирьох відрізків утворити чотирикутник, потрібно перевірити, чи буде найдовший з них меншим за суму трьох інших.

Кути чотирикутника називають протилежними, якщо їх вершини – протилежні вершини чотирикутника.

Сума кутів кожного чотирикутника дорівнює 360°.

Кут, суміжний з кутом чотирикутника, називають зовнішнім кутом чотирикутника.

При кожний вершини чотирикутника є два зовнішні кути, які рівні меж собою.

Сума зовнішніх кутів опуклого чотирикутника, взятих по одному при кожній вершині, дорівнює 360°.

Периметр чотирикутника – це сума довжин усіх його сторін.

Периметр позначають літерою P.

Периметр чотирикутника обчислюють за формулою:

P = AB + BC + CD + DA.

ЗАДАЧА:

У трикутнику АВС кут А дорівнює 56°, кути В і С – гострі. Висоти ВD і СЕ перетинаються в точці О. Знайдіть кут DОЕ.
РОЗВ'ЯЗАННЯ:

Оскільки сума кутів опуклого чотирикутника дорівнює 360°, то чотирикутника АЕОD:

∠ А + ∠ Е + ∠ О + ∠ D = 360°,

звідки

∠ DОЕ = ∠ О =

= 360° – 90° – 90° – 56° = 124°.

ЗАДАЧА:

У трикутнику АВС:

СЕ і ВF – висоти, що перетинаються у точці Т.

∠ ЕТВ = 31°.

Знайдіть ∠ А.
РОЗВ'ЯЗАННЯ:

∠ ЕТF = 180° – 31° = 149°.

Оскільки сума кутів опуклого чотирикутника дорівнює 360°, то чотирикутника АЕТF:

∠ А + ∠ АЕТ + ∠ АFТ + ∠ FТЕ = 360°,

звідки

∠ А = 360° – 90° – 90° – 149° = 31°.

ЗАДАЧА:

В чотирикутнику АВСD сторона ВС на 1 см, а сторона АD на 6 см більші за АВ. Знайдіть периметр чотирикутника, якщо довжина сторони СD є середнім арифметичним сторін АВ та

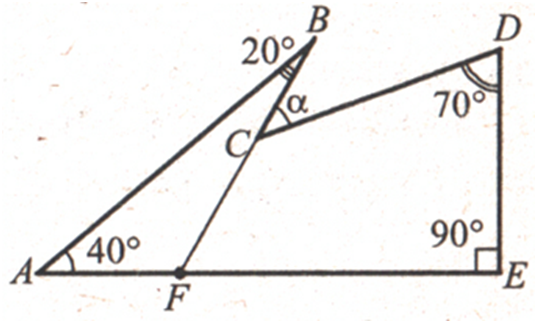
АD і СD = 5 см.

РОЗВ'ЯЗАННЯ:

Дано: чотирикутник АВСD.

ВС = (АВ + 1) см,

АD = (АВ + 6) см,

СD = 5 см.

Знайти: Р_АВСD.

Р_АВСD = AB + BC + CD + AD.

Із того, що

маємо:

2CD = AB + AD або

2 × 5 = AB + AB + 6;

2AB + 6 = 10; 2AB = 4;

AB = 2 см.

BC = AB + 1, BC = 3 см;

AD = AB + 6, AD = 8 см;

Р_АВСD = 2 + 3 + 5 + 8 = 18 см.

ВІДПОВІДЬ: 18 см.

ЗАДАЧА:

Визначте величину кута α, зображеного на рисунку.
РОЗВ'ЯЗАННЯ:

АВСDЕ – заданий многокутник. Продовжимо відрізок ВС до перетину з прямою АЕ,
∠ ВFЕ – зовнішній до трикутника АВF, тому

∠ ВFЕ = ∠ А + ∠ В =

= 40° + 20° = 60°.

У чотирикутнику FСDЕ

∠ С = 360° – 70° – 90° – 60° = 140°.

Тоді кут α = 180° – ∠ С =

= 180° – 140° = 40°.

ВІДПОВІДЬ: 40°.

ЗАДАЧА:

Знайдіть найменший з кутів чотирикутника, якщо величини його кутів пропорційні числам 2, 5, 6 і 7.

РОЗВ'ЯЗАННЯ:

Нехай найменший кут чотирикутника 2х, тоді решта кутів –

5х, 6х і 7х. Звідси:

2х + 5х + 6х + 7х = 360°,

20х = 360°, 2х = 36°.

Завдання до уроку 17

Інші уроки:

Уроки математики и физики для школьников и родителей

пятница, 28 ноября 2014 г.