Урок 11. Рівнобедрений (рівносторонній) трикутник (2).

среда, 1 октября 2014 г.

Урок 11. Рівнобедрений (рівносторонній) трикутник (2).

ВІДЕОУРОК
Бісектриса, висота та медіана рівнобедреного (рівностороннього) трикутника.

Властивості рівнобедреного трикутника.

– бісектриса, проведена до основи рівнобедреного трикутника, є його медіаною і висотою;

– висота рівнобедреного трикутника, проведена до основи, є одночасно його медіаною і бісектрисою;

– медіана рівнобедреного трикутника, проведена до основи, є одночасно його висотою і бісектрисою;
ВD – медіана, висота, бісектриса

– медіани, бісектриси та висоти, проведені до бічних сторін рівнобедреного трикутника, рівні.

Ознаки рівнобедреного трикутника.

– одна з висот є бісектрисою або медіаною;
– одна з медіан є висотою або бісектрисою;
– одна з бісектрис є медіаною або висотою;
– дві медіани (висоти, бісектриси) рівні.

Для будь – якого рівнобедреного трикутника

Висота, медіана та бісектриса, опущені на ту саму сторону, збігаються, якщо дві інші сторони трикутника рівні (трикутник рівнобедрений). Збіг двох цих ліній достатньо для встановлення рівнобедреності трикутника.

ЗАДАЧА:

У трикутнику АВС:

АС = ВС, висота СН = 4,

∠ АСВ = 30°.
Знайдіть ВС.

РОЗВ'ЯЗАННЯ:

Розглянемо прямокутний трикутник АСН. Катет, що лежить проти кута 30°, дорівнює половині гіпотенузи, отже,

АН = 0,5АС = 4,

АС = ВС = 8.

ЗАДАЧА:

У рівнобедреному трикутнику МКЕ (МК = КЕ) бісектриса кута Е перетинає сторону МК у точці С. Знайдіть кути трикутника, якщо ∠ КСЕ = 126°.

РОЗВ'ЯЗАННЯ:

Нехай ∠ Е = ∠ М = α, тоді у ∆ МКЕ

∠ К = 180° – 2α. З ∆ КСЕ:

∠ СЕК + ∠ К + ∠ С = 180°.

^α/₂ + 180° – 2α + 126° = 180°,

^3α/₂ α = 126°, α = 84°.

Отже,

∠ Е = ∠ М = 84°,

∠ К = 180° – 2 ∙ 84° = 12°.

ВІДПОВІДЬ:

84°, 84°, 12°.

ЗАДАЧА:

У трикутнику АВС:

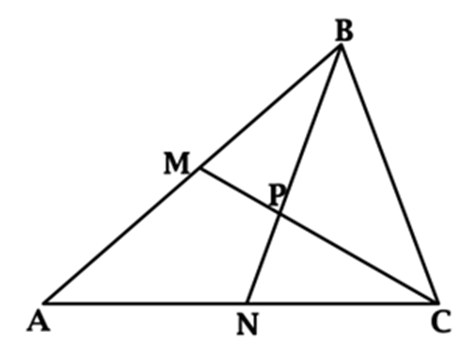
ВМ і СN – медіани, ВМ = СN,

О – точка перетину ВМ і СN,

∠ ОВС = 36°.
Знайдіть ∠ ВОС.

РОЗВ'ЯЗАННЯ:

У трикутнику медіани точкою перетину діляться щодо 2:1, рахуючи від вершини. Оскільки ВМ = СN, то

ВО = ²/₃ ВМ = ²/₃ СN = СО,

тоді трикутник ВОС – рівнобедрений. У рівнобедреному трикутнику кути при підставі рівні, тоді

∠ ОСВ = ∠ ОВС = 36°.

Оскільки сума кутів у трикутнику дорівнює 180°, то

∠ ВОС = 180° – ∠ ОВС – ∠ ОСВ =

= 180° – 36° – 36° = 108°.

ЗАДАЧА:

У трикутнику АВС:

ВN і СМ – медіани, АВ = 4,

О – точка перетину ВN і СМ,

∠ РВС = 35°, ∠ ВРС = 110°.
Знайдіть NС.

РОЗВ'ЯЗАННЯ:

Оскільки сума кутів у трикутнику дорівнює 180°, то

∠ РСВ = 180° – 110° – 35° =

= 35° = ∠ РВС,

отже трикутник РВС – рівнобедрений і РВ = РС.

У трикутнику медіани точкою перетину діляться щодо 2 : 1, рахуючи від вершини. Так як РВ = РС, то

МР = 0,5 ∙ РС = 0,5 ∙ РВ = РN.

Кути ∠ МРВ і ∠ NРС – вертикальні, а отже рівні.

Таким чином, трикутники МРВ та РNС – рівні (по двох сторонах та кутку між ними), тоді

NС = МВ = 0,5 ∙ АВ = 2.

ЗАДАЧА:

У трикутнику АВС:

ВF і AE – медіани, АE = BF,

О – точка перетину BF і AE,

∠ FOE = 147°.
Знайдіть ∠ ABO.

РОЗВ'ЯЗАННЯ:

∠ АОВ = ∠ FОЕ = 147° (як вертикальні).

У трикутнику медіани точкою перетину діляться щодо 2:1, рахуючи від вершини. Оскільки АЕ = ВF, то

АО = ²/₃ ∙ АЕ = ²/₃ ∙ ВF = ВО,

тоді трикутник АВО – рівнобедрений. У рівнобедреному трикутнику кути при підставі рівні, тоді

∠ ОАВ = ∠ АВО.

Оскільки сума кутів у трикутнику дорівнює 180°, то

180° = ∠ ОАВ + ∠ АВО + ∠ АОВ =

2 ∙ ∠ АБО + 147°,

звідки ∠ АВО = 16,5°.

ЗАДАЧА:

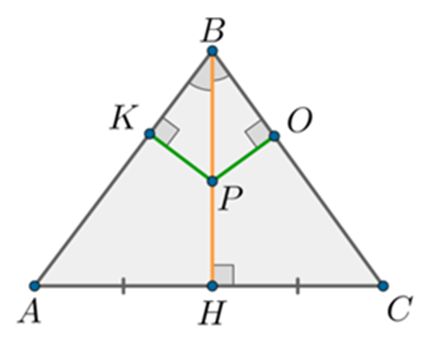
Знайдіть основу рівнобедреного трикутника, якщо кут при підставі дорівнює 30°, а взята всередині трикутника точка знаходиться на однаковій відстані, що дорівнює 3, від бічних сторін і на відстані 2√͞͞͞͞͞3 от основи.
РОЗВ'ЯЗАННЯ:

Точка Р знаходиться на рівній відстані від обох сторін трикутника, отже, лежить на бісектрисі ВН, бо АВ = ВС, то ВН теж є медіаною і висотою.

∠ АВС = 120°, отже ∠ АВН = ∠ КВР = 60°.

∆ КВР – прямокутний, отже ∠ ВРК = 30°, а проти кута в 30° лежить катет у 2 рази менше за гіпотенузу. Позначимо КВ = х, тоді ВР = 2х. Користуючись теоремою Піфагора, складемо рівняння.

4х² = х² + 9,

знаходимо х.

х = √͞͞͞͞͞3, тоді

ВР = 2√͞͞͞͞͞3,

ВН = ВР + РН =

= 2√͞͞͞͞͞3 + 2√͞͞͞͞͞3 = 4√͞͞͞͞͞3.

Так як у ∆АВН кут А = 30°,

то АВ = 2ВР = 8√͞͞͞͞͞3.

Тоді за теоремою Піфагора отримуємо:

АН² = АВ² – ВН² =

= (8√͞͞͞͞͞3)² – (4√͞͞͞͞͞3)² =

= 192 – 48 = 144.

АН = 12, тоді

АС = 2АН = 24.

ЗАДАЧА:

У рівнобедреному трикутнику АВС, у якому

АВ = ВС = 30,

АС = 48.
Знайдіть відстань між точкою перетину медіан і точкою перетину бісектрис.

РОЗВ'ЯЗАННЯ:

Оскільки трикутник АВС рівнобедрений, то ВК – медіана, висота та бісектриса. Тоді за теоремою Піфагора:

За якістю медіан точка М ділить медіани щодо 2 : 1, рахуючи від вершини, тоді

ВМ = 12, МК = 6.

За властивістю бісектрис АТ поділяє відрізок ВМ на частини, пропорційні прилеглим сторонам, тобто:

ТК = 8,

ТМ = ТК – КМ =

= 8 – 6 = 2.

Для прямокутного рівнобедреного трикутника

ЗАДАЧА:

У трикутнику АВС:

∠ С = 90°,

СЕ – медіана,

∠ АСЕ = 50°.
Знайдіть ∠ В.

РОЗВ'ЯЗАННЯ:

∠ ЕСВ = ∠ АСВ – ∠ АСЕ = 40°.

У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи. Тоді СЕ = ВЕ, отже трикутник СЕВ – рівнобедрений. У рівнобедреному трикутнику кути при підставі рівні, тоді

∠ В = ∠ ЕСВ = 40°.

ЗАДАЧА:

У прямокутному трикутнику гострий кут дорівнює 60°. Катет, що лежить проти цього кута, дорівнює 12 см.

Знайдіть бісектрису цього кута.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
Бісектриса кута в 60° ділить його на два кути по 30°. Тоді трикутник АВL – рівнобедрений. Позначивши невідому бісектрису за х, отримуємо:

АL = ВL = х. Тоді

СL = ВС – ВL = 12 – х.

Але СL – катет у трикутнику АВL, що лежить проти кута 30° і він дорівнює половині гіпотенузи, тобто

АL = 2СL.

Знаходимо х.

х = 2СL = 2(12 – х),

х = 24 – 2х,

3х = 24,

х = 8.

ЗАДАЧА:

Даний прямокутний трикутник АВС. З вершини А до сторони ВС проведено медіану АD і бісектрису АМ. Кут між медіаною та бісектрисою дорівнює 17°.
Знайдіть гострі кути трикутника.

РОЗВ'ЯЗАННЯ:

Оскільки АМ – бісектриса, то кут ВАМ дорівнює куту МАС і вони дорівнюють 45°. Але кут DАМ дорівнює 17°. Звідси, кут ВАD дорівнює різниці кутів ВАМ і DАМ:

45° – 17° = 28°.

Ми знаємо, що медіана, проведена з вершини прямого кута прямокутного трикутника, ділить цей трикутник на два рівнобедрених трикутники. А саме трикутники АВD та АDС. І тепер, оскільки трикутник АВD рівнобедрений, то кути при основі у нього рівні, тобто кут ВАD дорівнює куту АВD і вони обидва дорівнюють 28°. А це означає, що в прямокутному трикутнику кут дорівнює 28°. Звідси, кут С дорівнюватиме

90° – 28° = 62°.

Для рівностороннього трикутника

Будь-яка бісектриса рівностороннього трикутника буде його медіаною та висотою.

ЗАДАЧА:

У трикутнику АВС:

АВ = ВС = АС = 2√͞͞͞͞͞3.
Знайдіть висоту СН.

РОЗВ'ЯЗАННЯ:

Оскільки АС = ВС, то СН також є медіаною, отже,

АН = 0,5 АВ = √͞͞͞͞͞3.

Тоді за теоремою Піфагора з трикутника АСН знаходимо СН:

ЗАДАЧА:

У рівносторонньому трикутнику АВС, висота СН = 2√͞͞͞͞͞3.
Знайдіть основу АВ.

РОЗВ'ЯЗАННЯ:

Так як АС = ВС, то СН також є медіаною, отже,

АН = а, то АВ = АС = 2а.

Тоді за теоремою Піфагора з трикутника АСН знаходимо АВ:

АС² = АН² + СН²,

4а² = а² + 12,

а = 2, АВ = 2а = 4.

Завдання до уроку 11

Інші уроки:

Уроки математики и физики для школьников и родителей

среда, 1 октября 2014 г.