Урок 15. Прямокутний трикутник і коло.

суббота, 18 октября 2014 г.

Урок 15. Прямокутний трикутник і коло.

ВІДЕОУРОК

Вписане коло прямокутного трикутника.

Радіус кола, вписаного в прямокутний трикутник,

можна знайти за формулою:

де r – шуканий радіус, а і b – катети,

с – гіпотенуза трикутника.

Радіус вписаний у прямокутний трикутник кола

дорівнює добутку катетів, поділеному на суму катетів та гіпотенузи.

де r – радіус, а і b – катети,

с – гіпотенуза трикутника.

Радіус вписаного в прямокутний трикутник кола дорівнює площі цього трикутника, поділеного на півпериметр:

де р – напівпериметр

ЗАДАЧА:

Точка дотику кола, вписаного в прямокутний трикутник, ділить один з катетів на відрізки 2 см і 8 см, рахуючи від вершини прямого кута. Знайдіть периметр трикутника.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення:

ВМ = ВN = х.

(2 + х)² + (2 + 8)² = (8 + х)²,

х² + 4х + 4 + 100 =

= х² + 16х + 64,

12х = 40,

х = ¹⁰/₃ (см).

Р = (2 + 8) + (8 + ¹⁰/₃) + (¹⁰/₃ + 2) = 26²/₃ (см).

ЗАДАЧА:

Вписане коло прямокутного трикутника АВС дотикається до гіпотенузі АВ у точці К. Знайдіть радіус вписаного кола, якщо

АК = 4 см, ВК = 6 см.

РОЗВЯ'ЗАННЯ:

За властивістю дотичних маємо:

АК = АМ = 4 см,
ВК = ВN = 6 см.

Позначимо радіус вписаного кола через х:

СN = СM = NО = МО = х.

Тоді

АС = (4 + х) см,
ВС = (6 + х) см,

АВ = 4 см + 6 см = 10 см.

За теоремою Піфагора для трикутника АВС можна записати співвідношення:

(4 + х)² + (6 + х)² = 10².

Розв'яжемо це квадратне рівняння:

16 + 8x + x² + 36 + 12x + x² = 100,

2x² + 20x + 52 – 100 = 0,

2x² + 20x – 48 = 0,

x² + 10x – 24 = 0,

x₁ = 2, x₂ = –10.

x₂не задовольняє умову задачі.

ВІДПОВІДЬ: 2 см.

ЗАДАЧА:

Вписане коло прямокутного трикутника АВС дотикається до гіпотенузи АВ у точці К. Знайдіть радіус вписаного кола, якщо

АК = 4 см, ВК = 6 см.

РОЗВ'ЯЗАННЯ:

Нехай коло О радіуса х дотикається до катетів трикутника в точках М і N.
Оскільки ОМСN – квадрат, то

СМ = СN = х см.

За властивістю дотичних, проведених з однієї точки, одержимо:

А N = АК = 4 см,

ВМ = ВК = 6 см.

Розглянемо прямокутний трикутник АВС. У ньому:

АВ = 4 + 6 = 10 (см),

АС = (4 + х) см,

ВС = (6 + х) см.

За теоремою Піфагора маємо:

АС² + ВС² = АВ²,

(4 + х)² + (6 + х)² = 10²,

2х² + 20х + 52 = 100,

х² + 10х – 24 = 0,

х₁ = –12 – не підходить,

х₂ = 2.

Отже, радіус кола дорівнює 2 см.

ВІДПОВІДЬ: 2 см

ЗАДАЧА:

Точка дотику кола, вписаного в прямокутний трикутник, ділить гіпотенузу на відрізки 8 см і 12 см. Знайдіть периметр трикутника.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення:

(8 + 12)² = (8 + х)² + (12 + х)²,

400 = 64 + 16x + x² + x² + 24x + 144,

2x² + 40x – 192 = 0,

x² + 20x – 96 = 0,

x₁ = 4, x₂ = –24.

x₂не підходить.

Р = 8 + 12 + 12 + 4 + 4 + 8 = 48 (см).

ВІДПОВІДЬ: 48 см.

Описане коло прямокутного трикутника.

Центром кола, описаного навколо прямокутного трикутника, буде середина його гіпотенузи.

Діаметр кола, описаного навколо прямокутного трикутника, дорівнює його гіпотенузі.
Медіана прямокутного трикутника, проведена до його гіпотенузи, дорівнює половині гіпотенузи і є радіусом кола, описаного біля цього трикутника.

ОА = ОВ = ОС = R
Радіус описаного кола дорівнює половині гіпотенузи:

ЗАДАЧА:

Відрізок ВС – діаметр кола, зображеного на рисунку
Кут АВС = 55°.

Яка величина кута АСВ ?

РОЗВ'ЯЗАННЯ:

ВС – діаметр, тому ∠ ВАС = 90°,

∠ АСВ = 180° – (90° + 55°) = 35°.

ЗАДАЧА:

Перпендикуляр, опущений з точки кола на його діаметр, ділить діаметр на відрізки, різниця яких дорівнює 5 см. Знайдіть радіус кола, якщо довжина перпендикуляра дорівнює 6 см.

РОЗВ'ЯЗАННЯ:

Нехай АВ – діаметр кола з центром у точці О, СD ⊥ АВ,
де С – точка кола,

СD = 6 см, АD = х см,

ВD – АD = 5 см.

Тоді DВ = (х + 5) см. Трикутник АСВ – прямокутний (кут С прямий, бо він вписаний і спирається на діаметр).

СD – перпендикуляр, проведений з вершини прямого кута на гіпотенузу. Тоді:

АD ∙ DВ = СD²,

х(х + 5) = 6²,

х² + 5х – 36 = 0,

x₁ = –9, x₂ = 4.

x₁не підходить.

Отже, АD = 4 см,

DВ = 4 + 5 = 9 (см).

АВ = АD + DВ =

= 4 + 9 = 13 (см).

Тоді

r = АВ : 2 = 13 : 2 = 6,5 (см).

ВІДПОВІДЬ: 6,5 см

ЗАДАЧА:

З точки на колі проведено дві перпендикулярні хорди, різниця яких дорівнює 4 см. Знайдіть ці хорди, якщо радіус кола дорівнює 10 см.

РОЗВ'ЯЗАННЯ:

Нехай задане коло радіуса R,
у якому проведено хорди АВ і АС (АВ ⊥ АС),

R = АО = ВО = СО = 10 см,

АС – АВ = 4 см.

Нехай АВ = х см, тоді

АС = (4 + х) см.

Оскільки ∠ А = 90°, то трикутник ВАС – прямокутний, у якому

ВС = 2ОВ= 2 ∙ 10 = 20 см.

З прямокутного трикутника ВАС маємо:

АВ² + АС² = ВС²,

х² + (4 + х)² = 20²,

х² + 16 + 8х + х² = 400,

х² + 4х – 192 = 0,

х₁ = 12, х₂ = –16 – не підходить.

Отже, АВ = 12 см,

АС = 4 + 12 = 16 (см).

ВІДПОВІДЬ: 12 см, 16 см

ЗАДАЧА:

Кут між бісектрисою та медіаною прямокутного трикутника, проведеними з вершини прямого кута, дорівнює 14°. Знайдіть менший кут цього трикутника.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
Оскільки трикутник прямокутний і медіана ВМ виходить із прямого кута В, точка М є центром описаного кола навколо трикутника АВС. Отже,

АМ = МС = МВ = R,

де R – радіус описаного кола.

Знайдемо спочатку кут МВС. Враховуючи, що BD – бісектриса, то

∠ DВС = ⁹⁰/₂ = 45°. Тоді

∠ МВС = ∠ МВD + ∠ DВС,

∠ МВС = 14° + 45° = 59°.

Розглянемо рівнобедрений трикутник МВС зі сторонами

МВ = МС,

в якому кути при основі ВС рівні, тобто

∠ С = ∠ МВС = 59°.

Оскільки сума гострих кутів у прямокутному трикутнику дорівнює 90°, то

∠ А + ∠ С = 90°,

∠ А = 90° – ∠ С =

= 90° – 59° = 31°.

ЗАДАЧА:

Периметр прямокутного трикутника дорівнює 72 м, а радіус вписаного в нього кола – 6 м. Знайдіть діаметр описаного кола.

РОЗВ'ЯЗАННЯ:

DO = OF = OE = r = 6 м.

Отже AD = AF = 6 м.

FC = EC, BD = BE (відрізки дотичних, проведені з однієї точки)

Нехай BD = BE = x, FC = EC = y,

Тоді

AB = x + 6, AC = y + 6,
BC = x + y.

AB + AC + BC =
x + 6 + y + 6 + x + y = 72.

2x + 2y + 12 = 72,

2x + 2y = 60,

x + y = 30.

(x + y) – гіпотенуза, або діаметр описаного кола.

ВІДПОВІДЬ: 30 м

ЗАДАЧА:

У колі на відстані 6 см від його центра проведено хорду завдовжки 16 см. Чому дорівнює радіус кола ?

РОЗВ'ЯЗАННЯ:

Накреслимо креслення:

Користуючись теоремою Піфагора, знаходимо радіус.
ЗАДАЧА:

Два кола, радіуси яких дорівнюють 4 см і 9 см, мають зовнішній дотик. Знайдіть відстань між точками дотику даних кил з їх спільною зовнішньою дотичною.

РОЗВ'ЯЗАННЯ:

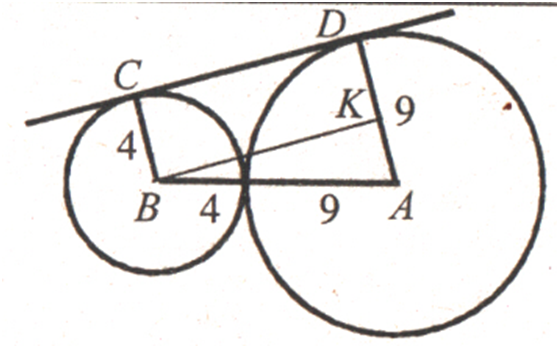
ВК ⊥ АD, АК = 9 – 4 = 5 см.

З ∆ ВКА:

СD = ВК = 12 см.

ЗАДАЧА:

У кут, величина якого становить 60°, вписано два кола, які зовнішньо дотикаються одно до одного. Знайдіть радіус більшого з них, якщо радіус меншого дорівнює 6 см.

РОЗВ'ЯЗАННЯ:
∠ СОА = 60°,

ОС = 2СА = 12 см,

∆ ОDВ:

ОD = 2DВ = 2R,

12 + 6 + R = 2R,

R + 18 = 2R,

R = 18 см.

ЗАДАЧА:

Бісектриса АМ трикутника АВС (∠ С = 90°) ділить катет ВС на відрізки завдовжки 6 см і 10 см. Знайдіть радіус кола, яке проходить через точки А, С, і М.
РОЗВ'ЯЗАННЯ:

АМ – бісектриса кута А, тому
Оскільки АВ ˃ АС, то

ВМ ˃ МС і

ВМ = 10 см, МС = 6 см.
Нехай АС = 6х, тоді АВ = 10х.

З прямокутного трикутника АВС (∠ С = 90°) маємо:

АВ² = АС² + ВС²,

(10х)² = (6х)²+ (10 + 6)²,

64х² = 16², х = 2 (см),

АС = 6х = 12 (см).

З прямокутного трикутника АСМ (∠ С = 90°) маємо:

АМ² = АС² + СМ²,

12² + 6², АМ = 6√͞͞͞͞͞5 (см).

Коло, яке проходіть через точки А, М і С, є описаним колом навколо прямокутного трикутника АСМ. Тоді його діаметр дорівнює гіпотенузі трикутника. Отже,

r = ¹/₂ АМ = 3√͞͞͞͞͞5 (см).

ЗАДАЧА:

У колі по різні боки від його центра проведено дві паралельні хорди, довжина яких дорівнює 6 см і 8 см, а відстань між ними – 4 см. Знайдіть радіус кола.

РОЗВ'ЯЗАННЯ:

Нехай задане коло О,

у якому проведено хорди АВ і СD,

АВ = 6 см, СD = 8 см.

Через точку О проведемо

FЕ ⊥ АВ.

АЕ = ВЕ = 3 см,

FЕ ⊥ СD,

СF = FD = 4 см,

ЕF = 4 см.

Трикутники ОВЕ і ОDF прямокутні, до того ж

ОВ = ОD = r.

Нехай ОF = х см, тоді ОЕ = ЕF – х = (4 – х) см. З прямокутного трикутника ОЕВ за теоремою Піфагора

ОВ² = ОЕ² + ВЕ²,

r² = (4 – х)² + 3².

Аналогічно

ОD² = ОF² + FD²,

r² = х² + 4².

(4 – х)² + 3² = х² + 4².

16 – 8х + х² + 9 = х² + 16,

8х = 9, х = ⁹/₈. Тоді
Завдання до уроку 15

Інші уроки:

Уроки математики и физики для школьников и родителей

суббота, 18 октября 2014 г.