ВІДЕОУРОКДва промені зі
спільним початком ділять площину на дві частини.
Кутом називають частину площини, обмежену двома променями зі спільним
початком.
Промені називаються сторонами
кута, а їх спільний початок – вершиною
кута.
Коротко записують:
∠
АОВ, (∠ ВОА).
Якщо
кут позначено
трьома буквами, то середня буква в його назві відповідає вершині кута.
Даний кут можна позначити лише назвою його вершини, наприклад
∠ О
Кут також позначають маленькими буквами грецького алфавіту:
α, β, γ
тощо, тоді знак кута не пишуть. Можна позначати кут цифрами:
∠ О
Кут також позначають маленькими буквами грецького алфавіту:
α, β, γ
тощо, тоді знак кута не пишуть. Можна позначати кут цифрами:
∠ 1,
∠ 2,
∠ 3 тощо.
Площина поділяється сторонами кута на внутрішню область кута і
зовнішню.
Два кута називаються рівними, якщо при накладанні вони
суміщаються.
Якщо сторони кутів утворені відрізками, то при рівності кутів рівність сторін може не зберігатися.
На прямій DС позначено точку О. Утворились два промені
– ОС і ОD. Ці промені виходять зі
спільного початку О, тому теж утворюють кут – ∠ DОС. Такий кут називається розгорнутим.Якщо сторони кутів утворені відрізками, то при рівності кутів рівність сторін може не зберігатися.
Розгорнутим кутом
називається такий, одна сторона якого є продовженням іншої.
Два кути, що мають спільну вершину і спільну сторону,
називаються прилеглими, якщо їх
внутрішні області не покривають одна одну.
При перетині двох прямих
утворюються 4 кути, менші за розгорнутий. Менший з кутів,
утворених при перетині двох прямих, називають кутом між двома прямими.
Два кути називають суміжними, якщо в них одна сторона спільна, а
дві інші – доповняльні промені.
На рисунку
∠1 і ∠2, ∠1 і ∠4,
∠2 і ∠3, ∠3 і ∠4
– суміжні кути.
∠1 і ∠2, ∠1 і ∠4,
∠2 і ∠3, ∠3 і ∠4
– суміжні кути.
Сума суміжних кутів дорівнює 180°.
Щоб побудувати кут, суміжний з даним, треба одну з сторін даного кута продовжити за його вершину.
– якщо один із суміжних кутів гострий, то інший тупий.
– якщо один із суміжних кутів тупий, то інший гострий;
– якщо два суміжні кути рівні, то вони прямі;
– якщо два кути рівні, то суміжні з ним кути теж рівні.
Внутрішній
промінь кута, якій ділить даний кут навпіл, називають бісектрисою кута.
Бісектриса кута ділить
його навпіл. Кожна точка бісектриси
не розгорненого кута рівновіддалена від прямих, що містять сторони кута.
Кожна точка, що
лежить усередині кута і рівновіддалена від сторін кута, лежить на його
бісектрисі. Бісектриси суміжних
кутів утворюють прямий кут.
Два кути називають вертикальними, якщо сторони одного кута є
доповняльними променями до сторін іншого кута.
Вертикальні кути утворюються при перетині двох
прямих. На рисунку
∠ 1 і ∠ 3,
∠ 2 і ∠ 4
– вертикальні кути.
Вертикальні кути рівні.
∠ 1 і ∠ 3,
∠ 2 і ∠ 4
– вертикальні кути.
Вертикальні кути рівні.
Дії
з кутами.
Якщо вершину і сторону одного кута сумістити з вершиною і
стороною іншого, а інші сторони цих кутів розмістити з однієї сторони від
суміщеної, то:
– перший кут менший від другого, якщо не суміщена сторона його
знаходиться всередині (у внутрішній області) другого;
– перший кут більший від другого, якщо не суміщена сторона його знаходиться у зовнішній області другого.
– перший кут більший від другого, якщо не суміщена сторона його знаходиться у зовнішній області другого.
Якщо вершину і сторону одного кута сумістити з вершиною і стороною іншого так, щоб їх внутрішні області не накладаються, то утворений не суміщеними сторонами кут називається сумою даних кутів.
Сума кількох кутів визначається аналогічно.
Вимірювання
кутів.
Відрізок характеризує його довжина. Так само кут
характеризує його міра.
Мірою кута є величина повороту
променя ОА навколо точки О як центра обертання.
Повним називається кут, одержаний при одному повному
обертанні променя ОА.
Точка А при цьому опише коло радіусом ОА.
Половина повного кута становить розгорнутий
кут. Четверта частина повного кута становить прямий
кут.
Один радіан – це такий центральний кут, дуга якого дорівнює
радіусу кола.
Позначають радіан скорочено – рад. Поворот
променя ОА на 1 рад – це такий
поворот, при якому точка А описує дугу, що дорівнює за довжиною
відрізку ОА.
Отже, в повному оберті 2π радіанів. Розгорнутий кут містить π = 3,14159… рад, а прямий кут має π/2 рад.
Поширена також градусна система вимірювання кутів.
Щоб виміряти кут, треба обрати одиницю вимірювання –
одиничний кут. Найчастіше роблять це так. Розгорнутий кут поділяють на 180 рівних частин і одну з них обирають за
одиничний кут. Його міру називають градусом. Для кожного кута можна визначити його
градусну міру. На практиці для порівняння кутів, як і відрізків, можна
скористатися способом накладання. Рівні
кути мають рівні градусні міри. Із двох кутів більшим є той, градусна міра
якого більша. Градусна міра кута дорівнює сумі градусних мір його частини.
Є такі одиниці вимірювання кутів:
–
1 градус. У перекладі з латинської gradus означає
ступінь, крок.
Записують 1° – це кут, що становить 1/360
частину повного кута. Дуга центрального кута 1° становить
1/360 частину кола.
–
1 хвилина – це 1/60 частина градуса. Записують 1';
–
1 секунда – це 1/60 частина
хвилини. Записують 1''.
Слово ’’мінута’’
походить від латинського minutes –
зменшений, малий, – що в даному випадку означає дрібнішу частину градуса, а
слово ’’секунда’’ походить від
латинського secunda –
другий, тобто другий (менший) поділ градуса.
ПРИКЛАД:
Кут
40
градусів 37 хвилин
і 15
секунд записують так:
40°37'15''.
В повному оберті 360°, що еквівалентно
до 2π рад.
Перехід
від градусного вимірювання до радіанного і навпаки здійснюється за формулами:
Кути вимірюються:
у
радіанах
(1 радіан ≈ 57°18');
(1 радіан ≈ 57°18');
у градах
(1 град ≈ 0,9°);
у румбах
(1 румб ≈ 11,29°).
Кути вимірюються транспортиром.
Розгорнутий кут містить 180°.
Кути, менші від розгорнутого, можна поділити на три види – прямі, гострі чи
тупі кути. Кут, що дорівнює 90°,
називають прямим. Кут, менший від 90°,
називають гострим, а більший за 90° – тупим.
Для вимірювання кутів і
дуг у найпростіших випадках застосовується прилад, який називається транспортиром.Задачі на побудову.
ЗАДАЧА:
Про
вершині N
на промені NM
побудувати кут, що дорівнює даному
∠ АВС.
З вершини
B описуємо
дугу pq довільного радіуса і тим самим радіусом з
центра N проводимо дугу, яка перетинає промінь NM у
точці Р. З точки
Р радіусом, що дорівнює відрізку pq, робимо засічку і знайдену точку Q
сполучаємо з вершиною N.
Кут
QNM
–
шуканий.
ЗАДАЧА:
Побудувати
кути, які дорівнюють 30°, 60°
і 90°.
З
кінців А
і В
довільного відрізка АВ як з центрів описуємо радіусом R = АВ
дві дуги. Точки їх перетину С і D сполучаємо
прямою, яка перетинає відрізок АВ в його середині О. Точку А
сполучаємо прямою з точкою С.
Тоді
∠ АСО
= 30°,
∠ САО
= 60°,
∠АОС = 90°.
ЗАДАЧА:
Даний ∠ ВАС
поділити пополам.
З вершини А довільним радіусом проводимо дугу DЕ. З точок D і Е перетину її з сторонами АВ і АС описуємо довільними радіусами дуги аb, сd. Точку їх перетину F сполучаємо з А; одержана пряма АF ділить ∠ ВАС пополам, тобто є його бісектрисою.
ЗАДАЧА:
Поділити
прямий кут на три рівні частини.
Довільним
радіусом проводимо дугу з центром у вершині
А
даного кута до її перетину в точках
М
і N
з його сторонами. Цим самим радіусом з точок М
і N
як з центрів на
дузі МN робимо
дві засічки K
і L, які сполучаємо з вершиною А.
∠ MAK = ∠
KAL
= ∠ LAN = 30°.
ЗАДАЧА:
Поділити
даний ∠ BAC на три рівні частини.
За
допомогою лінійки без поділок й циркуля точно виконати цю побудову, яку
називають трисекцією кута, не можна. Проте за допомогою циркуля і міченої
лінійки (тобто лінійки, на яку нанесено рівномірну шкалу, наприклад
міліметрові) трисекцію кута легко виконати таким чином. Довільним радіусом АС
описуємо з вершини кута A
коло. Продовжуємо АС за точку
А. Кладемо мічену лінійку так, щоб
вона проходила через В,
і обертаємо її навколо В,
поки відрізок ЕD
між колом і прямою АК не дорівнюватиме радіусу АС. Тоді ∠ EDF
є третя частина ∠ BAC . Це легко довести, користуючись
тим, що відповідно до побудови ∆DEA
рівнобедрений, а за теоремою про зовнішній кут трикутника
∠
BEA
= 2x;
∠ BAC = α =
x
+ 2x,
x = ∠ EDA.
Інші уроки:
- Урок 1. Точка і пряма
- Урок 3. Паралельні і перпендикулярні прямі
- Урок 4. Коло
- Урок 5. Кут і коло
- Урок 6. Трикутник (1)
- Урок 7. Трикутник (2)
- Урок 8. Прямокутній трикутник (1)
- Урок 9. Прямокутній трикутник (2)
- Урок 10. Рівнобедрений (рівносторонній) трикутник (1)
- Урок 11. Рівнобедрений (рівносторонній) трикутник (2)
- Урок 12. Периметр трикутника.
- Урок 13. Периметр рівнобедреного трикутника
- Урок 14. Трикутник і коло
- Урок 15. Прямокутний трикутник і коло
- Урок 16. Рівнобедрений трикутник і коло
- Урок 17. Чотирикутники
- Урок 18. Паралелограм
- Урок 19. Периметр паралелограма
- Урок 20. Прямокутник
- Урок 21. Периметр прямокутника
- Урок 22. Квадрат
- Урок 23. Ромб
- Урок 24. Периметр ромба
- Урок 25. Трапеція
- Урок 26. Рівнобічна трапеція
- Урок 27. Периметр трапеції
- Урок 28. Чотирикутник і коло (1)
- Урок 29. Чотирикутник і коло (2)
- Урок 30. Многокутник
- Урок 31. Правильний многокутник
- Урок 32. Осьова і центральна симетрії




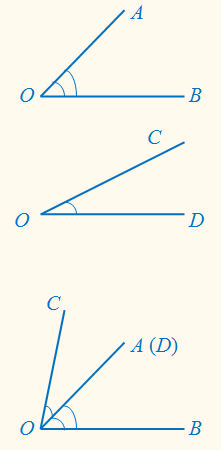







Комментариев нет:
Отправить комментарий