ВІДЕОУРОКОсновні
поняття.
Поверхню можна уявити як спільну частину двох
суміжних областей простору або як нескінченно тонкий шар, який відокремлює дві
суміжні частини простору. Поверхня не має товщини.
Лінія уявляється як спільна частина
(границя) двох суміжних ділянок поверхні. В результаті перетину двох поверхонь
ми одержуємо лінію. Лінія має лише один вимір – довжину.
Точка відокремлює одну від одної суміжні
частини лінії. Чітке уявлення про точки дають перетини ліній між собою і ліній
з поверхнями. Точка не має жодного виміру.
Площина – окремий вид поверхні, будь-яка
частина якої може бути суміщена з вихідною поверхнею в будь-якому її місці як у
прямому, так і перевернутому вигляді (властивість прямого і перевернутого
ковзання).
Пряма є окремим видом лінії. Якщо через
дві точки площини провести пряму лінію, то і всі точки цієї прямої будуть
знаходиться на площині. Уявлення про неї дає перетин двох площин.
Нескінченна пряма – пряма, яка
продовжується в обидві сторони нескінченно. Звичайно нескінченну пряму називають
просто прямою.
Промінь, або напівпряма – частина
прямої, обмежена лише з одного боку, тобто промінь є частиною прямої, яка
виходить їз заданої точки і прямує до нескінченності в даному напрямку.
Ламана лінія – лінія, утворена
відрізками прямих, які не лежать на одній прямій і розміщенні так, що кінець
першого відрізка є початком другого, кінець другого – початком третього і т.д. Відрізки
прямих, які утворюють ламану, називаються сторонами (ланками)
ламаної. Точки стику відрізків називаються вершинами ламаної. Ламана лінія
називається опуклою, якщо всі її ланки
розміщені по одну сторону від кожного відрізка, продовженого необмежено в
обидва кінці. Ламана називається замкненою,
якщо кінці її збігаються в одну точку. Точками само перетину ламаної лінії
називаються такі точки, в яких перетинаються її
ланки. Кінці ланок при цьому не враховуються.
Основними геометричними фігурами на площині є точка і пряма. Точки прийнято
позначати великими латинськими буква A, B, C, D,
… . Прямі позначаються малими латинськими буквами a,
b, c, d, … . Пряма нескінченна. На малюнку зображуємо лише
частину прямої, але уявляємо її необмежено продовженою в обидва боки. Пряму
можна позначити двома точками, що лежать на ній. Коли прямі на площині мають
дві спільні точки, то кажуть, що вони збігаються, а колі мають одну спільну
точку, тоді вони перетинаються.
Основними властивостями належності точок і прямих на
площині назвемо такі властивості:
Властивості
прямої.
– яка б не була пряма, існують точки, що
належать цій прямій, і точки, що не належать їй;
– через будь-які дві точки можна провести пряму і тільки одну;
– з трьох точок на прямій одна і тільки одна лежить між двома
іншими;
– якщо дві прямі накладені одна на одну так, що які-небудь дві
точки однієї прямої суміщаються з двома точками другої прямої, то ці дві прямі
суміщаються і в усіх інших точках;
– дві прямі можуть перетинатися лише в одній точці;
– пряма має властивість ковзання – будь-яка її ділянка може
ковзати нескінченно.
Відрізок.
Відрізком називається частина прямої, яка складається з усіх
точок цієї прямої, що лежать між двома даними її точками.
Ці точки називаються кінцями відрізка. Відрізок
позначають, записуючи його кінці. Коли говорять або пишуть відрізок
АВ,
то мають на увазі відрізок з кінцями в точках
А і В.
Рівність
і нерівність відрізків.
Два відрізки вважаються рівними, якщо при накладанні вони
суміщаються усіма точками.
Якщо на даному відрізку взяти дві точки, з яких хоча
б одна не збігається з його кінцем, то відрізок, обмежений цими точками,
називається частиною відрізка. Якщо один відрізок дорівнює частини другого, то
кажуть, що перший менший за другий, а другий – більший за перший. Відрізок
вважається орієнтованим, якщо
обумовлені його початок і кінець.
Додавання
і віднімання відрізків.
Додаванням (відніманням) відрізків називається
графічна операція, за допомогою якої на деякій прямій може бути побудований
відрізок, який є сумою даних відрізків (або відрізок – різниця відрізків
зменшуваного і від’ємника). Додавання відрізків слід відрізняти від додавання
довжин відрізків. В результаті додавання відрізків знаходимо довжину відрізка –
суми.
Сумою двох або кількох відрізків називається відрізок, побудований
на деякій прямій за доданками без їх взаємного накладання і без проміжків між
ними (стиковка відрізків).
Сума відрізків має переставну
і сполучну властивості.
Різницею двох відрізків називається відрізок, побудований шляхом
накладання меншого відрізка на більший так, щоб початки або кінці їх
суміщалися.
ПРИКЛАД:
Зайти
(побудувати) відрізок
AB
+ NM + PQ,
де AB,
NM и PQ
– дані відрізки.
На
довільній прямій від деякої точки R відкладемо у будь-яку сторону один з даних відрізків AB,
NM або PQ.
Далі на цій самій прямій відкладемо будь-який з відрізків, що залишилися, так,
щоб один з йог кінців сумістився з яким-небудь кінцем відкладеного відрізка, але
без накладання цих відрізків. Те само робимо з наступним відрізком.
ПРИКЛАД:
За
даною сумою двох відрізків і одним з відрізків-доданків
побудувати другий відрізок.
На
відрізку-сумі від будь-якого з кінців відкладемо даний відрізок-доданок. Відрізок,
що залишився, буде шуканим.
Множення
і ділення відрізків на число.
Помножити відрізок на ціле
додатне число n –
значить знайти суму n
таких відрізків. Одержаний в результаті відрізок є відрізком-добутком.
Поділити відрізок на ціле додатне число n
–
значить знайти такий відрізок, після множення якого на число n
одержимо даний відрізок.
Помножити цей відрізок на додатний раціональний дріб
m/n – значить помножити цей
відрізок на число m і одержаний відрізок поділити на n
частин. Можна виконати також спочатку
ділення на n,
а потім множення на m.
Довжина
відрізка.
Виміряти відрізок, сумірний з деяким відрізком, який
прийнято за один цю довжини, – значить узнати, скільки разів у ньому міститься
ця одиниця або яка-небудь її частина. Число, яке одержуємо в результаті
вимірювання, визначає довжину відрізка.
Довжиною відрізка, сумірного з одиницею довжини, називається
число, на яке треба помножити одиницю довжини, щоб одержати даний відрізок.
Це число раціональне.
Довжину відрізка виражають за допомогою іменованого
числа. Щоб знайти довжину відрізка, треба звести довжини його частин до однієї
одиниці вимірювання і отримані значення додати. Довжину відрізків вимірюють у
таких одиницях вимірювання:
1 мм, 1 см, 1 дм, 1 м, 1 км
тощо.
1 мм, 1 см, 1 дм, 1 м, 1 км
тощо.
Відрізки
називають рівними, якщо при накладанні вони суміщаються.
Рівні відрізки мають
однакові довжини, і навпаки, якщо довжини відрізків рівні, то рівні й самі
відрізки. Рівні відрізки позначають на рисунках однаковою кількістю рисок. Із
двох відрізків більшим є той, довжина якого більша. Відрізок коротший за будь –
яку іншу лінію, яка сполучає його кінці. Для вимірювання відрізків користуються різними вимірювальними
інструментами. Найпростішим таким інструментом є лінійка з поділками на ній. На
лінійці, якою ми користуємось для вимірювання відрізків, нанесено частину
числового променя. Вона утворює вимірювальну шкалу. Шкалу поділено штрихами на
рівні частини, які називаються поділками. Довжині кожної поділки відповідає
певна одиниця вимірювання. На лінійці довжина найменшої поділки відповідає 1
мм. Шкали можуть бути різної форми, і
вони є на різних вимірювальних приладах. На шкалі термометра кожній найменшій
поділці відповідає 1 градус.
Основними властивостями вимірювання відрізків назвемо
такі властивості:
– кожний відрізок має
певну довжину, більшу від нуля;
– довжина відрізка
дорівнює сумі довжин частин, на які він розбивається будь – якою його точкою.
Це означає, що коли на відрізку АВ взяти будь – яку точку С,
то довжина відрізка АВ дорівнює сумі довжин відрізків АС і ВС.
Довжину відрізка АВ
називають також відстанню між точками А і В.
Відношення
відрізків.
Відношенням двох відрізків називається відношення їх довжини,
виміряних за допомогою однієї і тієї самої одиниці довжини.
ПРИКЛАД:
Якщо відрізки АВ і СD мають довжини m і n, це записують так:
Зокрема, відношення відрізка до одиниці довжини чисельно дорівнює довжини відрізка. відношення двох відрізків не залежить від одиниці вимірювання.
Рівність двох відношень називається пропорцією.
Дві пари відрізків називаються пропорціональними, якщо відношення
відрізків однієї пари дорівнює відношенню відрізків другої пари.
Відрізок а називається середнім
пропорціональним відрізків
b і c,
якщо:
Відрізок
довжиною 24 см
поділено на три рівні частини. Знайти відстань між серединами першої и
третьої частин.
Шукана
відстань дорівнює довжині відрізка без суми довжин двох половин третьої частини
всього відрізка, тобто довжині всього відрізка без його третьої частини. Отже,
відстань між вказаними серединами дорівнює:
24 см –
24/3
см = 16 см.
Поділ
відрізка в даному відношенні.
Поділом відрізка AB деякою точкою N в даному відношенні
називається такий поділ, при якому відношення утворених в результаті відрізків AN і BN дорівнює даному відношенню, тобто має місце пропорція:
Ділення в заданому відношенні називається внутрішнім, якщо точка N лежить всередині відрізка AB, і зовнішнім – якщо точка N лежить на продовженні відрізка AB.
ПРИКЛАД:
Даний відрізок
AB поділити зовнішнім способом у відношенні 3/2.
Проводимо
через точку A довільну пряму і на ній від точки A
відкладаємо відрізок
AC
= 3a,
де а – довільний відрізок. Потім від
точки C
в сторону точки A відкладаємо відрізок
CD
= 2a.
Проводимо
відрізки
DB
і CN (CN ∥
DB).
Точка N
і буде шуканою, тобто вона ділить даний відрізок AB
зовнішнім способом у заданому відношенні, бо:
Відрізок можна продовжити за допомогою лінійки в
обидва боки. Якщо продовжимо відрізок АВ за його
кінець В необмежено, то дістанемо геометричну фігуру,
яку називають променем АВ.
Точка А
– початок променя АВ.
Кінця в променя немає. При позначенні променя на першому місці пишуть букву,
яка означає початок променя. Якщо продовжимо відрізок АВ за його кінець А,
то дістанемо промінь ВА,
початком якого є точка В. Якщо ми
продовжимо відрізок АВ
за обидва кінці необмежено, то дістанемо
фігуру, яку називають прямою.
Будь – яка точка прямої
ділить пряму на два промені, які мають спільний початок.
Пів прямою
або променем називають частину прямої, яка складається з усіх точок цієї
прямої, що лежать по один бік від даної на ній точки.
Ця точка називається
початковою точкою пів прямої. Різні пів прямі однієї й тієї самої прямої із
спільною початковою точкою називаються доповняльними. Пів прямі так само, як і
прямі, позначаються малими латинськими буквами. Можна позначити пів пряму двома
точками: початковою і ще якою-небудь точкою, яка належить пів прямій.
Початкову точку ставлять на першому місці. Пів пряму, наведену жирною лінією
можна позначити АВ.
Розглянемо тепер пів прямі з початковою
точкою С (пів прямі
СА і СВ). Точка С розділяє точки А і В. Тому точки
А і В не можуть належати одній пів прямій, отже,
пів прямі СА і СВ
доповняльні.
Точки, промені, відрізки і деякі інші геометричні фігури розміщуються на площині. Коли ми креслимо фігури, то частиною площини може бути, наприклад, аркуш зошита чи шкільна дошка. Площина не має країв, вона є <<необмеженою>> геометричною фігурою. Пряма розбиває площину на дві півплощини. Це розбиття має таку властивість. Якщо кінці якого-небудь відрізка належать одній півплощині, то відрізок не перетинає пряму. Якщо кінці відрізка належать різним півплощинам, то відрізок перетинає пряму.
Точки, промені, відрізки і деякі інші геометричні фігури розміщуються на площині. Коли ми креслимо фігури, то частиною площини може бути, наприклад, аркуш зошита чи шкільна дошка. Площина не має країв, вона є <<необмеженою>> геометричною фігурою. Пряма розбиває площину на дві півплощини. Це розбиття має таку властивість. Якщо кінці якого-небудь відрізка належать одній півплощині, то відрізок не перетинає пряму. Якщо кінці відрізка належать різним півплощинам, то відрізок перетинає пряму.
ЗАДАЧА
НА ПОБУДОВУ:
Поділити
даний відрізок пополам.
З кінців А і B даного відрізка АВ одним і тим
самим довільним, але більшим за половину відрізка АВ радіусом
R описуємо
дві дуги, які перетинаються у двох точках
С і D. Точки С і D
сполучаємо прямою СD. Точка N перетину
прямих АВ і СD є шукана
точка, яка ділить відрізок АВ пополам.
Завдання до уроку 1
Інші уроки:
- Урок 2. Кут
- Урок 3. Паралельні і перпендикулярні прямі
- Урок 4. Коло
- Урок 5. Кут і коло
- Урок 6. Трикутник (1)
- Урок 7. Трикутник (2)
- Урок 8. Прямокутній трикутник (1)
- Урок 9. Прямокутній трикутник (2)
- Урок 10. Рівнобедрений (рівносторонній) трикутник (1)
- Урок 11. Рівнобедрений (рівносторонній) трикутник (2)
- Урок 12. Периметр трикутника.
- Урок 13. Периметр рівнобедреного трикутника
- Урок 14. Трикутник і коло
- Урок 15. Прямокутний трикутник і коло
- Урок 16. Рівнобедрений трикутник і коло
- Урок 17. Чотирикутники
- Урок 18. Паралелограм
- Урок 19. Периметр паралелограма
- Урок 20. Прямокутник
- Урок 21. Периметр прямокутника
- Урок 22. Квадрат
- Урок 23. Ромб
- Урок 24. Периметр ромба
- Урок 25. Трапеція
- Урок 26. Рівнобічна трапеція
- Урок 27. Периметр трапеції
- Урок 28. Чотирикутник і коло (1)
- Урок 29. Чотирикутник і коло (2)
- Урок 30. Многокутник
- Урок 31. Правильний многокутник
- Урок 32. Осьова і центральна симетрії



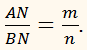







СПАСИБО!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
ОтветитьУдалитьЭтот комментарий был удален автором.
ОтветитьУдалить