Уроки математики и физики (RU + UA)

▼

вторник, 18 ноября 2014 г.

Урок 8. Сложение и вычитание многочленов

Сложение одночленов и многочленов.

 Чтобы сложить одночлены, достаточно записать их один за другим с их знаками и привести подобные члены, если они есть.

 ПРИМЕР:

 (–0,2ху) + (3,7х2) + (–3,5ху) + (–6,8х2) =
–0,2ху + 3,7х2 – 3,5ху – 6,8х2) = – 3,7ху – 3,1х2.  

ПРИМЕР:

Выполнить сложение одночленов:

18х2уz3  и  –8х2уz3.

 РЕШЕНИЕ:

18х2уz3 + (–8х2уz3) =
= (18 + (–8)) ∙ х2уz3 = 10х2уz3.

 ПРИМЕР:

 Суммой многочленов  

 а2 + ах + х3  и  с2 + сх + х  

 будет многочлен

 а2 + ах + х3 + с2 + сх + х.

 ПРИМЕР:

 Сложите многочлены

 х2 + 2х + 4, 3х2 – 4  и  3 – 2х.

 РЕШЕНИЕ:

х2 + 2х + 4 + 3х2 – 4 + 3 – 2х
= 4х2+ 3.

ПРИМЕР:

 (12а + 7b – c) + (c – 7b + 8a) = 
12а + 7b – c + c – 7b + 8a = 20a.

 Сложение расположенных многочленов выполняют так: подписывают многочлены так, чтобы подобные члены находились один под другим; после этого сразу приводят подобные члены и записывают окончательный результат.

 ПРИМЕР:

 Сложить многочлены:

3х4 + 7х3у – х2у2 – 5ху2;  
–7х4 – 5х3у + 8х2у2 + 10ху2;  
4х4 + 10х3у – 2х2у2 – 7ху2.
При  сложение многочленов можно применять арифметические законы сложения.
Для сложения многочленов применяются переместительный и сочетательный законы: какие бы не были многочлены  А, B  и  С, всегда

 А + B = B + А   и  
(А + B) + С = А + (B + С).

 Вычитание одночленов и многочленов.

 Чтобы вычесть одночлен, достаточно прибавить его к уменьшаемому с противоположным знаком и привести подобные члены, если они есть.

 ПРИМЕР:

 10а3 – (+7а3) = 
10а3 – 7а3 = 3а3;
–0,2m2n – (+7,3mn) 
= –0,2m2n – 7,3mn.

ПРИМЕР:

Упростить выражение:

18m – 13m.

РЕШЕНИЕ:

Пользуясь распределительным свойством умножения относительно вычитания, получим:

18m – 13m = m(18 – 13) =

= m∙ 5 = 5m.
Чтобы вычесть многочлен, надо записать после уменьшаемого все его члены с противоположными знаками и привести подобные члены, если они есть.

 ПРИМЕР:

 После первого многочлена пишут знак  << – >>, а второй берут в скобки. При раскрывании скобок, перед которыми стоит знак  << – >>, знаки всех членов, что были в этих скобках, заменяют на противоположные.

 (5х2 – 3ху + у2) – (6х2 – 8ху + у3) 
= 5х2 – 3ху + у2 – 6х2 + 8ху – у3
= – х2 + 5ху + у2 – у3.

ПРИМЕР:

10а3 – (+7а3) =

= 10а3 – 7а3 = 3а3;

–0,2m2n – (+7,3mn) =

= –0,2m2n – 7,3mn.
ПРИМЕР:

 Найдите разность многочленов  

 ab + c – 4  и  2ab + c – 3.

 РЕШЕНИЕ:

 ab + c – 4 – (2ab + c – 3) 
= ab + c – 4 – 2ab – c + 3 
= – ab – 1.

ПРИМЕР:

(5а + 5) – (2 + а) =

= 5а + 5 – 2 – а = 4а + 3.

ПРИМЕР:

6х – 5 – (9х – 8) =

= 6х – 5 – 9х + 8 = –3х + 3.

Вычитание расположенных многочленов можно выполнять так: у вычитаемого многочлена заменить знаки всех членов на противоположные, подписать его под уменьшаемым так же, как и при сложении, и привести подобные члены.

 ПРИМЕР:

 Выполнить вычитание в столбик:

(8х4 – 3х3 + 7х2 + х – 18) – (5х4 – 6х3 + 3х2 + 4х – 7).  

 РЕШЕНИЕ:
И сумма, и разность многочленов – многочлен. 

 Задания к уроку 8
Другие уроки:
на

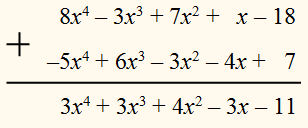
Комментариев нет:

Отправить комментарий