Сократить дробь – значит разделить её числитель и
знаменатель на их общий множитель.
Возможность такого
сокращения обусловлена основным свойством дроби. Если числитель и знаменатель
дроби многочлены, то их надо предварительно разложить на множители. Если
окажется, что числитель и знаменатель имеют общие множители, то дробь можно
сократить. Если общих множителей нет, то преобразование дроби посредством
сокращения дроби невозможно.
Примеры сокращения алгебраических дробей, если
в числителе и знаменателе дроби находятся одночлены.
Если числитель и
знаменатель дроби одночлены, то общие делители находят устно и затем сокращают.
ПРИМЕР:
ПРИМЕР:
Преобразуем числитель. Вынесем общий множитель за скобки:
8х2 – 40х + 32 = 8(х2 – 5х + 4) =
Воспользуемся способом группировки:
= 8(х2
– х – 4х + 4) =
= 8(х(х – 1) – 4(х – 1)) =
= 8(х – 1)(х – 4).
ПРИМЕР:
Имеем:
х2 – 3ху = х(х
– 3у).
9у2 – х2 = –(х2
– 9у2) =
= – (х – 3у)(х + 3у).
ПРИМЕР:
Необходимо квадратный трёхчлен разложить на множители:
х2 + 14х + 24.
РЕШЕНИЕ:
Разложим трёхчлен на множители, выделив с выражения
х2 + 14х + 24
квадрат двучлена.
Первый член есть квадрат числа х (первое число), второй член (14х) можно рассматривать как удвоенное произведение
первого числа на второе число, которое равно
7.
14 = 2 × х × 7.
Чтобы получить квадрат двучлена, прибавим квадрат второго
числа
72 = 49,
а чтобы числовое значение не изменилось, отнимем это же
самое число (49). Получим:
(х2 + 14х + 49) – 49 + 24 =
= (х + 7)2 – 25 = (х + 7)2 – 52.
Применив формулу разности квадратов, получим:
(х + 7 + 5)(х + 7 – 5) =
= (х + 12)(х + 2).
Окончательный ответ:
х2 + 14х + 24 = (х + 12)(х + 2).
Сокращение алгебраических
дробей с помощью разложения квадратного трёхчлена на множители.
ПРИМЕР:
Разложим квадратный трёхчлен на множители:
b2 + b –
12 =
= b2 + 2 ∙
0,5 ∙ b +
0,52 – 0,52 – 12 =
= b2 +
2 ∙ 0,5 ∙ b + 0,52 – 12,25 =
= (b + 0,5)2 – (3,5)2 =
= (b + 0,5 + 3,5)(b +
0,5 – 3,5) =
= (b + 4)(b –
3).
Числитель дроби разложим на множители с
помощью формулы разности квадратов:
b2 – 16 = (b +
4)(b –
4).
Разложим квадратный трёхчлен на множители:
а2 + а – 6 =
= а2 + 2 ∙
0,5 ∙ а + 0,52
– 0,52 – 6 =
= а2 + 2 ∙ 0,5 ∙ а + 0,52 – 6,25 =
= (а + 0,5)2 – (2,5)2
=
= (а + 0,5 + 3,5)(а + 0,5 – 3,5) =
= (а + 4)(а – 3).
Знаменатель дроби разложим на множители с
помощью формулы разности квадратов:
а2 – 9 = (а + 3)(а – 3).
Разложим квадратный трёхчлен на множители в
числителе:
х2 – 8х + 12 =
= х2 – 2 ∙ 4
∙ х + 42
– 42 + 12 =
= х2 – 2 ∙ 4 ∙ х + 42 – 4 =
= (х – 4)2 – (2)2 =
= (х – 4 + 2)(х – 4 – 2) =
= (х – 2)(х – 6).
Разложим квадратный трёхчлен на множители в
знаменателе:
х2 – 12х + 20 =
= х2 – 2 ∙ 6
∙ х + 62
– 62 + 20 =
= х2 – 2 ∙ 6 ∙ х + 62 – 16 =
= (х – 6)2 – (4)2 =
= (х – 6 + 4)(х – 6 – 4) =
= (х – 2)(х – 10).
Разложим квадратный трёхчлен на множители:
4а2 + а – 3 =
= а2 + 0,25а – 0,75 =
= а2 + 2 ∙
0,125 ∙ а + 0,1252
– 0,1252 – 0,75 =
= а2 + 2 ∙ 0,125 ∙ а + 0,1252 – 0,765625 =
= (а + 0,125)2 – (0,875)2
=
= (а + 0,125 + 0,875)(а + 0,125 – 0,875) =
= (а + 1)(а – 0,75) = (а + 1)(4а – 3).
Числитель дроби разложим на множители с
помощью формулы разности квадратов:
а2 – 1 = (а + 1)(а – 1).
Разложим квадратный трёхчлен на множители в
знаменателе:
2а2 – 11а – 6 =
= а2 – 5,5а – 3 =
= а2 – 2 ∙
2,75 ∙ а + 2,752
– 2,752 – 3 =
= а2 – 2 ∙ 2,75 ∙ а + 2,752 – 10,5625 =
= (а – 2,75)2 – (3,25)2
=
= (а – 2,75 + 3,25)(а – 2,75 – 3,25) =
= (а – 0,5)(а – 6) = (2а – 1)(а – 6).
Числитель дроби разложим на множители с
помощью формулы квадрата разности двух чисел:
а2 – 12а + 36 = (а – 6)2.
Разложим квадратный трёхчлен на множители:
5а2 – 16а + 3 =
= а2 – 3,2а + 0,6 =
= а2 – 2 ∙
1,6 ∙ а + 1,62
– 1,62 + 0,6 =
= а2 – 2 ∙ 1,6 ∙ а + 1,62 – 1,96 =
= (а – 1,6)2 – (1,4)2
=
= (а – 1,6 + 1,4)(а – 1,6 – 1,4) =
= (а – 0,2)(а – 3) =
= (а – 3)(5а – 1).
Числитель дроби разложим на множители с
помощью формулы разности кубов:
а3 – 27 = (а –
3)(а2 + 3а + 9).
a4 + a2b2 + b4 + a2b2 – a2b2
=
= a4 + 2a2b2 + b4 – a2b2 =
= (a2 + b2)2 – a2b2 =
= (a2 + b2
– ab)( a2 + b2
+ ab).
Преобразуем знаменатель дроби. Сгруппируем
члены многочлена следующим образом:
a3 + b3
+ 2a2b + 2ab2 =
= (a3 + b3) + 2ab(а + b) =
= (а + b)(a2 + b2 – ab) + 2ab(а +
b) =
= (а + b)(a2 + b2 – ab + 2ab) =
= (а + b)(a2 + b2 + ab).
- Урок 1. Рациональные алгебраические выражения
- Урок 2. Тождественные выражения
- Урок 3. Одночлены
- Урок 4. Умножение одночленов
- Урок 5. Возведение в степень одночленов
- Урок 6. Деление одночленов
- Урок 7. Многочлены
- Урок 8. Сложение и вычитание многочленов
- Урок 9. Умножение одночлена на многочлен
- Урок 10. Умножение многочленп на многочлен
- Урок 11. Вынесение общего множителя за скобки
- Урок 12. Способ группировки
- Урок 13. Произведение суммы двух чисел на их разность
- Урок 14. Разность квадратов двух чисел
- Урок 15. Квадрат суммы и квадрат разности двух чисел
- Урок 16. Преобразование многочлена в квадрат суммы или квадрат разности двух выражений
- Урок 17. Сумма и разность кубов двух чисел
- Урок 18. Куб суммы и куб разности двух чисел
- Урок 19. Применение различных способов разложения многочлена на множители
- Урок 20. Алгебраические дроби
- Урок 21. Сокращение дробей (1)
- Урок 23. Сложение алгебраических дробей
- Урок 24. Вычитание алгебраических дробей
- Урок 25. Умножение алгебраических дробей
- Урок 26. Деление алгебраических дробей
- Урок 27. Возведение алгебраических дробей в целую положительную степень
- Урок 28. Возведение алгебраических дробей в целую отрицательную степень
- Урок 29. Преобразование алгебраических выражений
































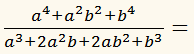


Комментариев нет:
Отправить комментарий