Выражение, состоящее из чисел и переменных с помощью действий сложения, вычитания, умножения, деления или возведения в степень, называется алгебраическим.
ПРИМЕР:Иногда возникает потребность упростить громоздкие дробные выражения. Это можно сделать на основании уже известных правил действий над дробями и целыми выражениями. Каждое алгебраическое дробное выражение можно представить в виде дроби, а некоторые – даже в виде целого выражения.Преобразование
любого алгебраического выражения можно свести к сложению, вычитанию, умножению
иди делению алгебраических дробей, а также к возведению дроби в целую степень. Из
правил действий с дробями следует, что сумму, разность, произведение и частное дробей
всегда можно представить в виде дроби. Значит, и всякое алгебраическое
выражение можно представить в виде алгебраической дроби, числитель и знаменатель которой – целые выражения. В
этом, как правило, состоит цель тождественных преобразований алгебраических
выражений.
Упростить выражение:
Решение вторым способом (цепочкой):
Разложим знаменатели на множители
a2 + 2a +
1 = (a +
1)2,
a2 – 2a + 1 =
(a – 1)2,
a2 – 1 = (a –
1)(a + 1).
Общий знаменатель равен
(a – 1)2(a + 1)2.
- Урок 1. Рациональные алгебраические выражения
- Урок 2. Тождественные выражения
- Урок 3. Одночлены
- Урок 4. Умножение одночленов
- Урок 5. Возведение в степень одночленов
- Урок 6. Деление одночленов
- Урок 7. Многочлены
- Урок 8. Сложение и вычитание многочленов
- Урок 9. Умножение одночлена на многочлен
- Урок 10. Умножение многочленп на многочлен
- Урок 11. Вынесение общего множителя за скобки
- Урок 12. Способ группировки
- Урок 13. Произведение суммы двух чисел на их разность
- Урок 14. Разность квадратов двух чисел
- Урок 15. Квадрат суммы и квадрат разности двух чисел
- Урок 16. Преобразование многочлена в квадрат суммы или квадрат разности двух выражений
- Урок 17. Сумма и разность кубов двух чисел
- Урок 18. Куб суммы и куб разности двух чисел
- Урок 19. Применение различных способов разложения многочлена на множители
- Урок 20. Алгебраические дроби
- Урок 21. Сокращение дробей (1)
- Урок 22. Сокращение дробей (2)
- Урок 23. Сложение алгебраических дробей
- Урок 24. Вычитание алгебраических дробей
- Урок 25. Умножение алгебраических дробей
- Урок 26. Деление алгебраических дробей
- Урок 27. Возведение алгебраических дробей в целую положительную степень
- Урок 28. Возведение алгебраических дробей в целую отрицательную степень
















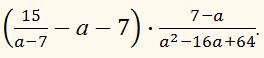








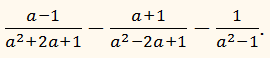





Комментариев нет:
Отправить комментарий