Приведение
алгебраических дробей к общему знаменателю выполняется так же, как и в
арифметике. При нахождении общего знаменателя у обыкновенных дробей мы находили
наименьшее общее кратное знаменателей, раскладывая их на простые множители.
Аналогично для нахождения общего знаменателя алгебраических дробей может
оказаться удобным разложение знаменателей на множители. Простейшим общим
знаменателем дробей с одночленными знаменателями есть наименьшее общее кратное
коэффициентов знаменателей (если они – натуральные числа), умноженное на все
различные буквы, входящие в знаменатели, причём каждую букву берут с наибольшим
показателем, с каким она входит в знаменатели.
Общим знаменателем нескольких рациональных дробей
называют целое рациональное выражение, которое делится на знаменатель каждой
дроби.
ПРИМЕР:
(х + 2)(х – 2) = х2 –
4,
2(х2 – 4), х(х2
– 4).
Общий знаменатель, на который делится любой другой
общий знаменатель без остатка, называется наименьшим общим знаменателем.
В приведённом
примере наименьшим общим знаменателем будет многочлен х2 – 4.
ПРИМЕР:
Так как
35y3
= 7y × 5y2,
ПРИМЕР:
Дополнительные множители следующие:
6а2b2 :
ab = 6ab,
6а2b2 :
3a2b =
2b,
6а2b2 :
2а2b2 =
3.
ПРИМЕР:
В данном примере наименьший общий знаменатель равен
(х + 2)(х – 2).
Чтобы несколько
рациональных дробей привести к общему знаменателю, нужно:
– разложить знаменатель каждой дроби на множители;
– составить общий знаменатель, включив в произведение
все множители, полученные в результате разложений, если некоторый множитель
имеется в нескольких разложениях, то он берётся с показателем степени, равным
наибольшему из имеющихся;
– найти дополнительные множители для каждой из дробей
(для этого общий знаменатель делят на знаменатель дроби);
– домножив числитель и знаменатель каждой дроби на
соответствующий дополнительный множитель, привести дроби к общему знаменателю.
ПРИМЕР:
(a – b), (a + b), а2,
а также наименьшее общее кратное чисел 12,
18, 24, то есть
(12, 18, 24) = 72.
Значит, общий знаменатель имеет вид:
72а2 ∙ (a – b)(a + b).
- Урок 1. Рациональные алгебраические выражения
- Урок 2. Тождественные выражения
- Урок 3. Одночлены
- Урок 4. Умножение одночленов
- Урок 5. Возведение в степень одночленов
- Урок 6. Деление одночленов
- Урок 7. Многочлены
- Урок 8. Сложение и вычитание многочленов
- Урок 9. Умножение одночлена на многочлен
- Урок 10. Умножение многочленп на многочлен
- Урок 11. Вынесение общего множителя за скобки
- Урок 12. Способ группировки
- Урок 13. Произведение суммы двух чисел на их разность
- Урок 14. Разность квадратов двух чисел
- Урок 15. Квадрат суммы и квадрат разности двух чисел
- Урок 16. Преобразование многочлена в квадрат суммы или квадрат разности двух выражений
- Урок 17. Сумма и разность кубов двух чисел
- Урок 18. Куб суммы и куб разности двух чисел
- Урок 19. Применение различных способов разложения многочлена на множители
- Урок 20. Алгебраические дроби
- Урок 22. Сокращение дробей (2)
- Урок 23. Сложение алгебраических дробей
- Урок 24. Вычитание алгебраических дробей
- Урок 25. Умножение алгебраических дробей
- Урок 26. Деление алгебраических дробей
- Урок 27. Возведение алгебраических дробей в целую положительную степень
- Урок 28. Возведение алгебраических дробей в целую отрицательную степень
- Урок 29. Преобразование алгебраических выражений
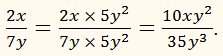




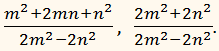



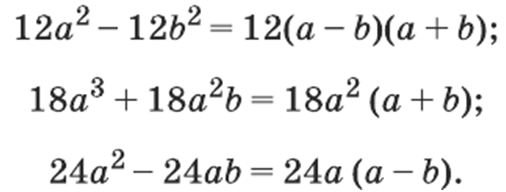

Комментариев нет:
Отправить комментарий