Вы знаете правило
отнимания обыкновенных дробей с одинаковыми знаменателями. Это правило можно выразить таким равенством:
Вычитание дробей с одинаковыми
знаменателями.
Разность
двух (и вообще любого конечного числа) алгебраических дробей с одинаковыми
знаменателями тождественно равна дроби с тем же знаменателем и с числителем,
равным разности числителей складываемых дробей:Чтобы вычесть алгебраические дроби с одинаковыми
знаменателями, надо вычесть их числители, а знаменатель оставить тот же самый.
ПРИМЕР:
Сложим дроби:
Теперь можно применять правило вычитания дробей с
одинаковыми знаменателями:
Вычитание дробей с
одинаковыми знаменателями.
Используя основное
свойство дроби, можно вычитание дроби с разными знаменателями привести до
вычитания с одинаковыми знаменателями. Пусть надо вычесть две алгебраические
дроби:
Можно записать:
Тогда
Тут за общий знаменатель выбрано выражение,
которое равно произведению знаменателю данных дробей. Отметим, что произведение
знаменателей данных дробей не всегда будет наибольшим общим делителем знаменателя.
Напомним, что при нахождении общего знаменателя у обыкновенных дробей мы
находили наименьшее общее кратное знаменателей, раскладывая их на простые
множители. Аналогично для нахождения общего знаменателя алгебраических дробей
может оказаться удобным разложение знаменателей на множители.Для вычитания алгебраических дробей с разными
знаменателями нужно, прежде всего, привести дроби к общему знаменателю, а затем
выполнить операции над полученными дробями с одинаковыми знаменателями.
Иногда возникает необходимость найти разность дроби и целого выражения. Их можно отнимать, как дроби, записав целое выражение в виде дроби со знаменателем 1.
ПРИМЕР:
Иногда возникает необходимость найти разность дроби и целого выражения. Их можно отнимать, как дроби, записав целое выражение в виде дроби со знаменателем 1.
ПРИМЕР:
Подобным способом упрощают
выражения, которые состоят из трёх или больше дробей, соединённых знаками плюс или
минус.
ПРИМЕР:
Выполните вычитание:РЕШЕНИЕ:ПРИМЕР:
Известно,
что
a/b = 5.
Другие уроки:
- Урок 1. Рациональные алгебраические выражения
- Урок 2. Тождественные выражения
- Урок 3. Одночлены
- Урок 4. Умножение одночленов
- Урок 5. Возведение в степень одночленов
- Урок 6. Деление одночленов
- Урок 7. Многочлены
- Урок 8. Сложение и вычитание многочленов
- Урок 9. Умножение одночлена на многочлен
- Урок 10. Умножение многочленп на многочлен
- Урок 11. Вынесение общего множителя за скобки
- Урок 12. Способ группировки
- Урок 13. Произведение суммы двух чисел на их разность
- Урок 14. Разность квадратов двух чисел
- Урок 15. Квадрат суммы и квадрат разности двух чисел
- Урок 16. Преобразование многочлена в квадрат суммы или квадрат разности двух выражений
- Урок 17. Сумма и разность кубов двух чисел
- Урок 18. Куб суммы и куб разности двух чисел
- Урок 19. Применение различных способов разложения многочлена на множители
- Урок 20. Алгебраические дроби
- Урок 21. Сокращение дробей (1)
- Урок 22. Сокращение дробей (2)
- Урок 23. Сложение алгебраических дробей
- Урок 25. Умножение алгебраических дробей
- Урок 26. Деление алгебраических дробей
- Урок 27. Возведение алгебраических дробей в целую положительную степень
- Урок 28. Возведение алгебраических дробей в целую отрицательную степень
- Урок 29. Преобразование алгебраических выражений


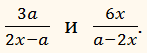
















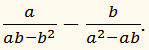







Комментариев нет:
Отправить комментарий