Уроки математики и физики (RU + UA)

▼

среда, 24 сентября 2014 г.

Урок 8. Прямокутній трикутник (1).

ВІДЕОУРОК
Прямокутним називають трикутник, у якого один з кутів є прямим.

Сторона прямокутного трикутника, що лежить навпроти прямого кута – називається гіпотенузою, а дві інші сторони – катетами. У кожному прямокутному трикутнику гіпотенуза більша за кожен катет.

Ознаки рівності прямокутних трикутників.

– якщо катети одного прямокутного трикутника дорівнюють відповідно катетам іншого прямокутного трикутника, то такі трикутники рівні;

– якщо катет і гострий кут одного прямокутного трикутника дорівнюють відповідно катету і гострому куту іншого прямокутного трикутника, то такі трикутники рівні;

– якщо гіпотенуза й гострий кут одного прямокутного трикутника дорівнюють відповідно гіпотенузі й гострому куту іншого прямокутного трикутника, то такі трикутники рівні;

– якщо гіпотенуза  й катет одного прямокутного трикутника дорівнюють відповідно гіпотенузі й катету іншого прямокутного трикутника, то такі трикутники рівні.
Якщо  АNМ – прямокутний трикутник із прямим кутом  N, його катет  АN – перпендикуляр, проведений з точки  А  на пряму  NМ. Гіпотенузу  АМ  називають також похилою, проведеною з точки  А  до прямої  NМ, а катет  NМ – проекцією цієї похилої на пряму  NМ. Будь-який трикутник можна розрізати на два прямокутні трикутники, а для кожного прямокутного трикутника справедлива теорема Піфагора.

Якщо трикутнику  АNМ  кут  N – прямий, то

NМ2 + АN2 = АМ2.

Теорема  Піфагора.

У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
Теорема, обернена до теоремі Піфагора. Якщо квадрат сторони трикутника дорівнює сумі квадратів двох інших його сторін, то цей трикутник – прямокутний.
Якщо  в трикутнику зі сторонами  а, b  і  с  справджується нерівність

c2 > a2 + b2

то кут, протилежний стороні  с, тупий.

Властивості прямокутних трикутників

– сума гострих кутів прямокутного трикутника дорівнює  90°;
– у прямокутному трикутнику гіпотенуза більша від катета;
– катет прямокутного трикутника, якій лежить проти кута  30°, дорівнює половині гіпотенузі.

Справедливе й обернене твердження: якщо катет прямокутного трикутника дорівнює половині гіпотенузи, то кут, протилежний цьому катету, дорівнює  30°.                                          
З теореми Піфагора випливає, що в прямокутному трикутнику будь – який з катетів менший за гіпотенузу.
З теореми Піфагора випливає, що коли з даної точки до прямої проведено перпендикуляр і похилі, то

 – будь – яка похила більша від перпендикуляра;
– рівні похилі мають рівні проекції;
– з двох похилих більша та, у якої проекція більша.

Піфагорові трикутники – прямокутні трикутники, довжини сторін яких виражаються цілими числами.

Наприклад, трикутники зі сторонами 

5, 12  і  13;  8, 15  і  17;  7,  24  і  25 

є піфагоровими.

Єгипетський трикутник – трикутник із сторонами  3, 4, 5.

ЗАДАЧА:

Визначте вид трикутника  АВС, якщо

∠ А = 37°, ∠ В = 53°.

РОЗВ'ЯЗАННЯ:

∠ С = 180° – (37° + 53°) =

= 180° – 90° = 90°,

тому трикутник  АВС – прямокутний.

ЗАДАЧА:

Визначте вид трикутника стороні якого дорівнюють 

26 см, 24 см, 10 см.

РОЗВ'ЯЗАННЯ:

Оскільки

242 + 102 = 576 + 100 =

= 676 = 262,

то трикутник прямокутний.

ЗАДАЧА:

Дано:  ∆ АВС, 

 ∠ С = 90°, 
АС = 3 см, 
ВС = 5 см.

 Знайти:  АВ.

РОЗВ'ЯЗАННЯ:

 АВ2 = АС2 + ВС2,
ВІДПОВІДЬ:
ЗАДАЧА:

Дано:  ∆ АВС, 

 ∠ С = 90°, 
АВ = 10 см, 
ВС = 5 см.

 Знайти:  АС.

РОЗВ'ЯЗАННЯ:

АВ2 = АС2 + ВС2,
ВІДПОВІДЬ:

ЗАДАЧА:

Знайдіть катет прямокутного трикутника, якщо його іншій катет і гіпотенуза відповідно дорівнюють  1 см, √͞͞͞͞͞17 см.

РОЗВ'ЯЗАННЯ:
ЗАДАЧА:

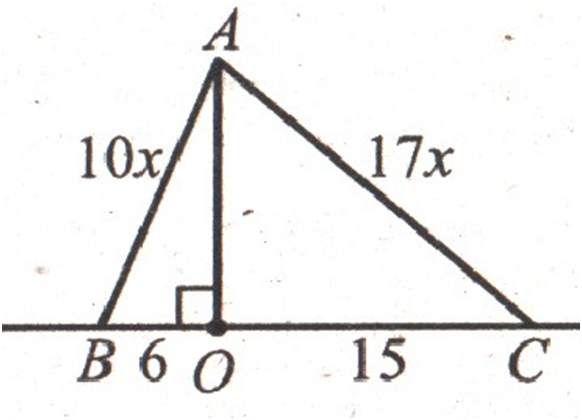
З точки до прямої проведено дві похилі, довжини проекцій яких на цю пряму дорівнюють  6 см  і  15 см. Знайдіть довжини похилих, якщо вони відносяться як  10 : 17.

РОЗВ'ЯЗАННЯ:

Намалюємо креслення.
Складемо пропорцію
Нехай  АВ = 10х, тоді  АС = 17х.

З  ∆ АОС (∠ О = 90°),

АО2 = АС2 – ОС2 =

= 289х2 – 225.

З  ∆ АОВ (∠ О = 90°),

АО2 = АВ2 – ВО2 =

= 100х2 – 36.

Звідси:

289х2 – 225 = 100х2 – 36,

289х2 = 289, х2 = 1, х = 1.

Отже,

АВ = 10 ∙ 1 = 10 (см),

АС = 17 ∙ 1 = 17 (см).

ЗАДАЧА:

З точки до прямої проведено дві похилих лінії завдовжки  13 см  і  15 см. Знайдіть відстань від цієї точки до прямої, якщо різниця цих проекцій похилих на пряму дорівнює  4 см.

РОЗВ'ЯЗАННЯ:

Намалюємо креслення.
КС – ВК = 4 см.

Нехай  ВК = х,

тоді  КС = х + 4.

З  ∆ АКВ (∠ К = 90°),

АК2 = АС2 – КС2 =

= 225 – (х + 4)2.

Звідки:

169 – х2 = 225 – х2 – 8х – 16,

8х = 40, х = 5 (см)

Отже, ВК = 5 см,
Завдання до уроку 8
Інші уроки:
на

Комментариев нет:

Отправить комментарий