Уроки математики и физики (RU + UA)

▼

пятница, 28 ноября 2014 г.

Урок 19. Периметр паралелограма

ВІДЕОУРОК
Периметр паралелограма – це сума довжин усіх його сторін.

Периметр позначають літерою  P. Периметр паралелограма обчислюють за формулою:

ЗАДАЧА:

Довжини сторін паралелограма відносяться як  3 : 4, а його периметр дорівнює  70 см. Знайдіть меншу сторону паралелограма.

РОЗВ'ЯЗАННЯ:

Нехай одна сторона паралелограма  3х см, тоді інша – 4х см.

На підставі формули
 
запишемо:

Р = 2(3х + 4х),

70 = 14х, х = 5.

Тоді  3х = 3 ∙ 5 = 15 (см).

ЗАДАЧА:

Бісектриса одного з кутів паралелограма ділить його сторону навпіл. Знайдіть периметр паралелограма, якщо ця сторона дорівнює  а см.

РОЗВ'ЯЗАННЯ:

Нехай  АВСК – даний паралелограм, тоді  

 ВС = АК = а  

як протилежні сторони паралелограма. АВ = ВР  як бічні сторони рівнобедреного трикутника  АВР, що відтинається бісектрисою кута паралелограма.
За умовою

ВР = РС = а/2.

Отже,

АВ = а/2  і  СК = а/2 

як протилежні сторони паралелограма.
Тому периметр паралелограма дорівнює:

а + а + а/2 + а/2 = 3а.

ВІДПОВІДЬ:  3а.

ЗАДАЧА:

Периметр паралелограма дорівнює  122 см. Одна з його сторін більша за іншу на  25 см. Знайдіть сторони паралелограма.

РОЗВ'ЯЗАННЯ:

Позначимо одну сторону паралелограма  х, іншу – у.

Отримаємо систему:
Вирішуючи цю систему, отримаємо:

х = 43, у = 18.

Сторони паралелограма дорівнюють  18 см  і  43 см.

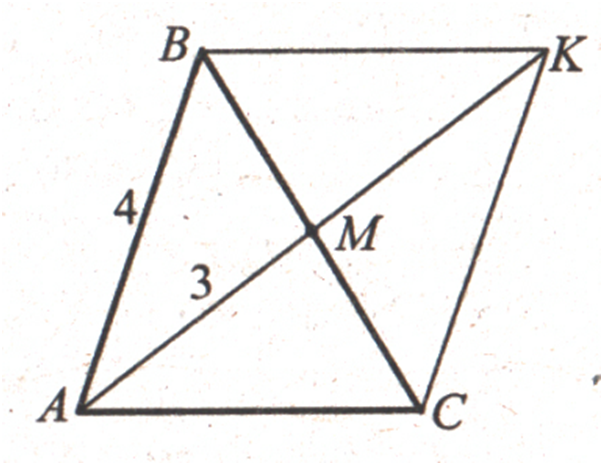
ЗАДАЧА:

Бічна сторона рівнобедреного трикутника дорівнює  4 см, а медіана, проведена до цієї сторони, – 3 см. Знайдіть периметр трикутника.

РОЗВ'ЯЗАННЯ:

Нехай  АВС – заданий трикутник,
у якого 

АВ = ВС = 4 см,

АМ – медіана,

АМ = 3 см,

На продовженні медіани  АМ  побудуємо точку  К  так, щоб 

АМ = МК.

Тоді 

АК = 2АМ = 6 (см).

У чотирикутнику  АВКС  діагоналі  ВС  і  АК  точкою перетину діляться навпіл. За ознакою цей чотирикутник – паралелограм. Одержимо:

ВС2 + АК2 = 2(АВ2 + АС2),

Знайдемо  АС:

42 + 62 = 2(42 + АС2),

2АС2 = 20, АС = √͞͞͞͞͞10.

Тепер знайдемо периметр трикутника:

Р = 2АВ + АС =

= (8 + √͞͞͞͞͞10) (см).

ЗАДАЧА:

У паралелограмі  ABCD  бісектриса кута  D  ділить сторону  ВС  на відрізки 

ВМ = 6 см,

МС = 3,2 см.

Знайдіть периметр паралелограма.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення:
∠ АDМ = ∠ МDС,

∠ АDМ = ∠ DМС 

як внутрішні різносторонні кути при перетині паралельних прямих  АD  і  ВС  січною  DМ. Отже,

∠ МDС = ∠ СМD  і 

∆ DСМ – рівнобедрений,

СD = СМ = 3,2 см.

ВС = ВМ + МС =

= 6 + 3,2 = 9,2 (см).

Р = 2(СD + ВС) =

= 2(3,2 + 9,2) = 24,8 (см).

 Завдання до уроку 19
Інші уроки:
на

Комментариев нет:

Отправить комментарий