Уроки математики и физики (RU + UA)

▼

суббота, 20 августа 2022 г.

Урок 28. Чотирикутник і коло (1)

ВІДЕОУРОК

 

Якщо всі вершини чотирикутника лежать на колі, його називають вписаним у коло, а коло – описаним навколо чотирикутника.

Навколо чотирикутника можна описати коло тоді й тільки тоді, коли суми його протилежних кутів дорівнюють  180°.
Якщо сума двох протилежних кутів опуклого чотирикутника дорівнює суми двох інших його кутів, то такий чотирикутник можна вписати в кола.

Якщо сума двох протилежних сторін опуклого чотирикутника дорівнює суми двох інших його сторін, то такий чотирикутник можна описати навколо кола.
AB = a, BC = b,

CD = c, DA = d. 

a + c = b + d                

У чотирикутник можна вписати коло тоді й тільки тоді, коли суми його протилежних сторін рівні:

a + c = b + d                

Не в кожний чотирикутник можна вписати коло і не навколо кожного чотирикутника – описати коло.

ЗАДАЧА:

Чому дорівнює кут  АDС  чотирикутника  ABCD, вписаного в коло, якщо 

∠ АСD = 32°,

∠ СВD = 56°.
РОЗВ'ЯЗАННЯ:

∠ 1 = ∠ СВD = 56°  (спираються на одну дугу  DС). З  ∆ АСD:

56° + 32° + ∠ АDС = 180°,

∠ АDС = 180° – 88° = 92°.

ЗАДАЧА:

Навколо кола описано чотирикутник  АВСD, у якого 

АВ = 14 см,

ВС = 16 см,

АD = 18 см.

Знайдіть довжину сторони  СD.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
AB + CD = AD + ВC,

CD = AD + ВC – AВ =

=18 + 16 – 14 = 20 (см).

ЗАДАЧА:

Чотирикутник  АВСD  вписаний в коло. Діагональ  АС  даного чотирикутника є діаметром кола. Знайдіть кут між діагоналями чотирикутника, що лежить проти сторони  AD, якщо 

∠ ВАС = 23°,

∠ DАС = 52°.

РОЗВ'ЯЗАННЯ:

Нехай  ABCD – даний чотирикутник, вписаний в коло, АС – діаметр кола. Отже,

∠ B =∠ D = 90°.

Нехай  К – точка перетину діагоналей чотирикутника, тоді шуканий кут – АКD. Кути  ВАС  і  ВDС  спираються на одну й ту саму дугу та лежать з одного боку від хорди  ВС. Отже,

∠ BDC =∠ DAC = 23°.

Оскільки  ∠ D = 90°, то

∠ ADK = 90° – ∠ BDC = 90° – 23° = 67°.

У трикутнику AKD

∠ AKD = 180° – (∠ KAD + ∠ ADK)

= 180° – (52° + 67°) = 61°.

ВІДПОВІДЬ:  61°

ЗАДАЧА:

Центр кола, описаного навколо чотирикутник  АВСD, належіть його стороні  СD. Знайдіть кути даного чотирикутника, якщо

∠ АВD = 34°, ∠ ВАС = 41°.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
∠ ВDС = ∠ ВАС = 41°

як вписані кути, які спираються на одну дугу.

З прямокутного трикутника  DВС (∠ В = 90°):

∠ С = 90° – 41° = 49°.

Аналогічно 

∠ АСD = ∠ АВD = 34°,

∠ D = 90° – 34° = 56°,

∠ А = ∠ DАС + ∠ САВ =

= 90° + 41° = 131°,

∠ В = ∠ АВD + ∠ DВС =

= 34° + 90° = 124°.

ВІДПОВІДЬ:

56°, 49°, 131°, 124°.

ЗАДАЧА:

Діагональ  ВD  чотирикутника  АВСD  є діаметром його описаного кола, М – точка перетину його діагоналей,

∠ АВD = 32°, ∠ СВD = 64°.

Знайдіть кут  ВМС.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
∠ А = 90°,

∠ 1= 90°– 32°= 58°,

∠ 2 = ∠ 1 = 58°,

∠ 3 = 180°– 64° – ∠ 2 =

= 180°– 64° – 58° = 58°

Прямокутник та коло.

Навколо будь – якого  прямокутника можна описати коло. Центром кола, описаного навколо прямокутника, є точка перетину його діагоналей.
ЗАДАЧА:

В коло вписаний прямокутник із сторонами  32  і  24. Знайти радіус кола.

РОЗВ'ЯЗАННЯ:

Діагональ  Д  цього прямокутника є діаметром кола, тоді, по теоремі Піфагора:
Радіус рівний  40 : 2 = 20.

ВІДПОВІДЬ:  20

Квадрат та коло.

У чотирикутник можна вписати коло тоді й тільки тоді, коли суми його протилежних сторін рівні:

a + c = b + d                

Не в кожний чотирикутник можна вписати коло і не навколо кожного чотирикутника – описати коло.

У будь – якій квадрат можна вписати коло й навколо квадрата     можна описати коло.
Центром вписаного й описаного кіл є точка перетину діагоналей квадрата
Формули для знаходження радіусу описаного кола.
Формули для знаходження радіусу вписаного кола.
ЗАДАЧА:

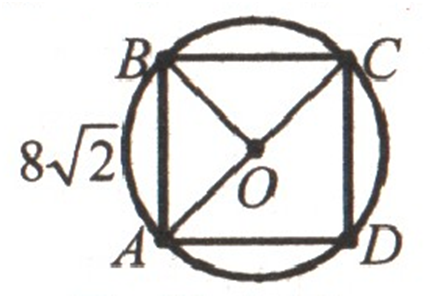
Чому дорівнює радіус кола, описаного навколо квадрата зі стороною  8√͞͞͞͞͞2 см ?

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
Скористаємося формулою:
ЗАДАЧА:

Чому дорівнює довжина кола, вписаного в квадрат зі стороною  10 см ?

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
r = 1/2 OE = 1/2 AB =

= 1/2 ∙ 10 = 5 (см),

l = 2πr = 2π ∙ 5 = 10π (см).

ЗАДАЧА:

Діагональ квадрата дорівнює   6√͞͞͞͞͞2 см. Чому дорівнює радіус вписаного в цей квадрат кола ?

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
Розглянемо трикутник  ОЕС. Він прямокутний та рівнобедрений. ОЕ – радіус вписаного кола. Позначимо його через  х  і скористаємося теоремою Піфагора:

х2 + х2 = (6√͞͞͞͞͞2 : 2)2,

2х2 = (3√͞͞͞͞͞2 )2,

х2 = 18 : 2 = 9,

х = 3 (см).

Завдання до уроку 28
Інші уроки:

на

Комментариев нет:

Отправить комментарий