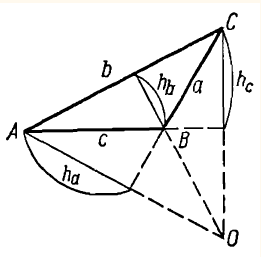
Ортоцентр О остроугольного треугольника лежит в середине треугольника.
Высоты треугольника, опущенные на стороны а, b, с, обозначаются соответственно через ha, hb, hc и вычисляются по формулам
– полупериметр треугольника.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
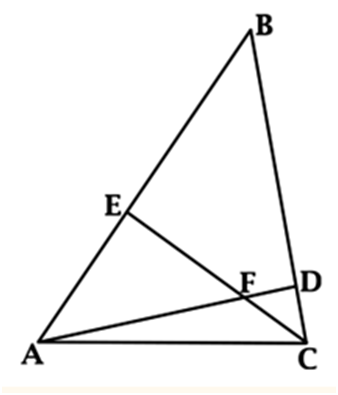
∠ AFE = 180° – ∠ EFD =
76°, тогда
∠ FAE = 90° – ∠ AFE =
14°
(так как
∠ FEA = 90°).
В треугольнике ADC, угол D = 90°, значит
∠ С = 90° – ∠ FAE =
90° – 14° = 76°.
ЗАДАЧА:
∠ FТС
= 180° – ∠ СТВ
= 28°, тогда
∠ ТСF =
90° – ∠ FТС
= 62°
(так как
∠ ТEС
= 90°).
В треугольнике AЕC, угол Е = 90°,
значит
∠ А
= 90° – ∠ ТСF =
90° – 62° = 28°.
ЗАДАЧА:
В треугольнике AЕC, угол Е = 90°, ∠ А = 60°,
тогда ∠ АСЕ = 90° – 60° = 30°.
Аналогично в
треугольнике АDС находим, что
∠ DАС
= 10°.
Так как сумма углов треугольника равна 180°, то
∠ АFС =
180° – 10° – 30° = 140°.
Углы АFС и ЕFD равны как
вертикальные, тогда ∠ EFD = 140°.
ЗАДАЧА:
В треугольнике ВОЕ, угол Е = 90°, ∠ ОВЕ = 19°,
тогда ∠ ВОЕ = 90° – 19° = 71°.
В треугольнике АВС сторона ВС равна 14 см, АC – 12 см. Найти сторону АВ, если АD – биссектриса и DС равно 8 см.
РЕШЕНИЕ:
– по свойству биссектрисы треугольника.
ОТВЕТ: 9 см.
В треугольнике АВС
∠ А = 60°, ∠ В = 80°.
Так как сумма углов треугольника равна 180°, поэтому
∠ С будет равен:
∠ С = 180° – 80° – 60° = 40°.
Биссектриса делит ∠ ВАС пополам,
значит ∠ DАС равен 30°.
Тогда
∠ АDС будет равен
110°.
ОТВЕТ:
∠ С = 40°,
∠ DАС =
30°,
∠ АDС =
110°.
ЗАДАЧА:
Отрезок АМ – биссектриса треугольника АВС,
АВ = 30 см, АС = 40 см,
СМ – ВМ = 5
см.
Найдите ВС.
РЕШЕНИЕ:
ВМ = х, СМ = х + 5.
ВС = х + х + 5 = 35 (см).
ЗАДАЧА:
∠
АКР = ∠
РКQ, так как они вертикальные.
∠
КАВ = 0,5 ∙ ∠ САВ,
∠
АВК = 0,5 ∙ ∠ АВС,
тогда при учёте т ого, что сумма углов в
треугольнике равна 180°
(∠ САВ + ∠
АВС + ∠ С
= 180°).
∠
КАВ + ∠
АВК =
= 0,5∙ (∠ САВ + ∠
АВС) =
= 0,5∙ (180° – 75°) = 52,5°, значит,
∠ АКВ
= 180° – (∠ КАВ + ∠
АВК) =
= 180° – 52,5° = 127,5°.
Таким образом,
∠
РКQ = 127,5°.
Медиана
треугольника.
Медианою
треугольника называется отрезок, который соединяет вершину треугольника с
серединой противоположной стороны. Каждый треугольник имеет три медианы.
Медианы любого треугольника
пересекаются в одной точке, которая находится в середине треугольника и
называется центроидом (центр масс или центр тяжести).
Медиану обозначают
буквою m.
AN – медиана, ВL – медиана, CM – медиана.
AO : ON = BO : OL =
CO : OM = 2 : 1
ЗАДАЧА:
AM = MN,
MN = NC,
тогда
AC = AM + MN + NC = 3MN,
AC = AM : MN = 3.
ЗАДАЧА:
В треугольнике АВС заданы медианы
ma, mb, mc.
Найти стороны треугольника.
РЕШЕНИЕ:
Обозначим стороны треугольника
АВ = с, АС = b, ВС = а.
- Урок 1. Точка и прямая
- Урок 2. Угол
- Урок 3. Параллельные и перпендикулярные прямые
- Урок 4. Окружность
- Урок 5. Угол и окружность
- Урок 6. Треугольник (1)
- Урок 8. Прямоугольный треугольник (1)
- Урок 9. Прямоугольный треугольник (2)
- Урок 10. Равнобедренный треугольник (1)
- Урок 11. Равнобедренный треугольник (2)
- Урок 12. Периметр треугольника
- Урок 13. Периметр равнобедренного (равностороннего) треугольника
- Урок 14. Треугольник и окружность
- Урок 15. Прямоугольный треугольник и окружность
- Урок 16. Равнобедренный треугольник и окружность
- Урок 17. Четырёхугольники
- Урок 18. Параллелограмм
- Урок 19. Периметр параллелограмма
- Урок 20. Прямоугольник
- Урок 21. Периметр прямоугольника
- Урок 22. Квадрат
- Урок 23. Ромб
- Урок 24. Периметр ромба
- Урок 25. Трапеция
- Урок 26. Равнобедренная трапеция
- Урок 27. Периметр трапеции
- Урок 28. Четырёхугольник и окружность (1)
- Урок 29. Четырёхугольник и окружность (2)
- Урок 30. Многоугольник
- Урок 31. Правильный многоугольник
- Урок 32. Осевая и центральная симметрии








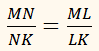

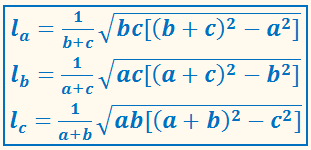


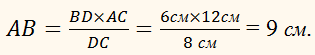






















Комментариев нет:
Отправить комментарий