Урок 17. Четырёхугольники

понедельник, 19 ноября 2018 г.

Урок 17. Четырёхугольники

ВИДЕОУРОК

Четырёхугольник – геометрическая фигура, состоящая из четырёх точек, каждые три из которых не лежат на одной прямой, и отрезков, последовательно их соединяющих, отрезки не должны пересекаться.
На рисунку точки А, В и С лежат на одной прямой, значит это не четырёхугольник.

На рисунку прямые АD и ВС пересекаются, значит это не четырёхугольник.

Точки называют вершинами четырёхугольника, отрезки – сторонами.

Смежные стороны четырёхугольника – стороны с общей вершиной.

Противоположные стороны четырёхугольника – пары несмежных сторон.

Противоположные вершины четырёхугольника – вершины, не соединённые общей стороной.

Диагональ четырёхугольника – отрезок, соединяющий противоположные вершины.

Каждая диагональ выпуклого четырёхугольника разделяет его на два треугольника.

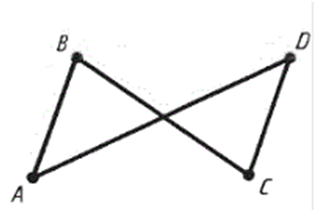
Четырёхугольник обозначают, записывая его вершины.

Четырёхугольник на рисунку обозначен следующим образом:

ABCD – выпуклый четырёхугольник.

В записи четырёхугольника вершины, которые стоят рядом, должны быть соседними. Четырёхугольник ABCD можно обозначить BCDA или CDAB, но нельзя обозначать ABDС (B и D – не соседние вершины).

AB, BC, CD, DA – стороны четырёхугольника; A, B, C, D – вершины четырёхугольника; AC и BD – диагонали.

Сумма углов выпуклого четырёхугольника равна 360°.

ЗАДАЧА:

В треугольнике АВС угол А равен 56°, углы В и С – острые. Высоты ВD и СЕ пересекаются в точке О. Найдите угол DОЕ.
РЕШЕНИЕ:

Так как сумма углов выпуклого четырёхугольника равна 360°, то для четырёхугольника АЕОD:

∠ А + ∠ Е + ∠ О + ∠ D = 360°,

откуда

∠ DОЕ = ∠ О =

= 360° – 90° – 90° – 56° = 124°.

ЗАДАЧА:

В треугольнике АВС: СЕ и ВF – высоты, пересекаются в точке Т. ∠ ЕТВ = 31°. Найдите ∠ А.
РЕШЕНИЕ:

∠ ЕТF = 180° – 31° = 149°.

Так как сумма углов выпуклого четырёхугольника равна 360°, то для четырёхугольника АЕТF:

∠ А + ∠ АЕТ + ∠ АFТ + ∠ FТЕ = 360°,

откуда

∠ А = 360° – 90° – 90° – 149° = 31°.

ЗАДАЧА:

В четырёхугольнике АВСD сторона ВС на 1 см, а сторона АD на 6 см больше чем АВ. Найдите периметр четырёхугольника, если длина стороны СD будет средним арифметическим сторон

АВ и АD и СD = 5 см.

РЕШЕНИЕ:

Дано: четырёхугольник АВСD.

ВС = (АВ + 1) см,
АD = (АВ + 6) см,
СD = 5 см.

Найти: Р_АВСD.

Р_АВСD = AB + BC + CD + AD.

Из того, что

получим:

2CD = AB + AD или

2 × 5 = AB + AB + 6;

2AB + 6 = 10; 2AB = 4;

AB = 2 см.

BC = AB + 1, BC = 3 см;

AD = AB + 6, AD = 8 см;

Р_АВСD = 2 + 3 + 5 + 8 = 18 см.

ОТВЕТ: 18 см.

ЗАДАЧА:

Определите величину угла α, изображённого на рисунку.
РЕШЕНИЕ:

АВСDЕ – заданный многоугольник. Продолжим отрезок ВС до пересечения с прямой АЕ,
∠ ВFЕ – внешний до треугольника АВF, поэтому

∠ ВFЕ = ∠ А + ∠ В =

= 40° + 20° = 60°.

В четырёхугольнике FСDЕ

∠ С = 360° – 70° – 90° – 60° = 140°.

Тогда угол

α = 180° – ∠ С =

= 180° – 140° = 40°.

ОТВЕТ: 40°.

ЗАДАЧА:

Найдите наименьший из углов четырёхугольника, если величины его углов пропорциональны числам 2, 5, 6 и 7.

РЕШЕНИЕ:

Пусть наименьший угол четырёхугольника 2х, тогда остальные углы –

5х, 6х і 7х. Звідси:

2х + 5х + 6х + 7х = 360°,

20х = 360°, 2х = 36°.

Задания к уроку 17

Другие уроки:

Уроки математики и физики для школьников и родителей

понедельник, 19 ноября 2018 г.