четверг, 12 февраля 2015 г.

Урок 11. Равнобедренный треугольник (2)

ВИДЕОУРОК
Биссектриса, высота и медиана равнобедренного (равностороннего) треугольника.

Свойства равнобедренного треугольника.

– биссектриса, проведённая до основания равнобедренного треугольника, будет его медианой и высотой;

– высота равнобедренного треугольника, проведённая до основания, будет одновременно его медианой и биссектрисой;

– медиана равнобедренного треугольника, проведенная до основания, будет одновременно его высотой и биссектрисой;
ВD – медиана, высота, биссектриса

– медианы, биссектрисы и высоты, проведённые до боковых сторон равнобедренного треугольника, равны.

Признаки равнобедренного треугольника.

– одна из высот будет биссектрисой или медианой;

– одна из медиан будет высотой или биссектрисой;

– одна из биссектрис будет медианой или высотой;

– две медианы (высоты, биссектрисы) равны.

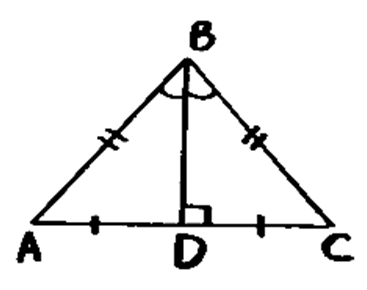
Для любого равнобедренного треугольника

Высота, медиана и биссектриса, опущенные на одну и ту же сторону, совпадают, если две другие стороны треугольника равны (треугольник равнобедренный). Совпадение двух из этих линий достаточно для установления равнобедренности треугольника.                                                  

ЗАДАЧА:

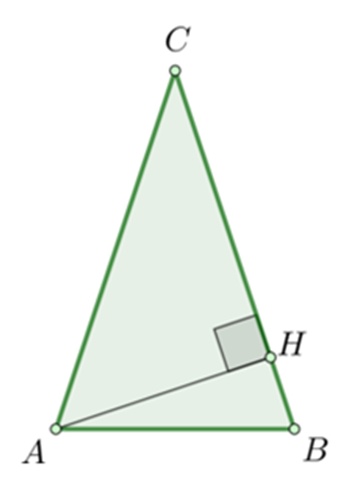
В треугольнике  АВС:

АС = ВС, высота  СН = 4,

∠ АСВ = 30°.
Найдите  ВС.

РЕШЕНИЕ:

Рассмотрим прямоугольный треугольник  АСН. Катет, лежащий против угла  30°, равен половине гипотенузы, следовательно,

 АН = 0,5АС = 4,

АС = ВС = 8.

ЗАДАЧА:

В равнобедренном треугольнике  МКЕ (МК = КЕ)  биссектриса угла  Е  пересекает сторону  МК  в точке  С. Найдите углы треугольника, если  ∠ КСЕ = 126°.
РЕШЕНИЕ:

Пусть  ∠ Е = ∠ М = α, тогда у  ∆ МКЕ 

∠ К = 180° – 2α. Из  ∆ КСЕ:

∠ СЕК + ∠ К + ∠ С = 180°.

α/2 + 180° – 2α + 126° = 180°,

3α/2 α = 126°, α = 84°.

Поэтому,

∠ Е = ∠ М = 84°,

∠ К = 180° – 2 ∙ 84° = 12°.

ОТВЕТ:

84°, 84°, 12°.

ЗАДАЧА:

В треугольнике  АВС:

ВМ  и  СN – медианы, ВМ = СN,

О – точка пересечения  ВМ  и  СN,

∠ ОВС = 36°.
Найдите ∠ ВОС.

РЕШЕНИЕ:

В треугольнике медианы точкой пересечения делятся в отношении  2 : 1, считая от вершины. Так как  ВМ = СN, то 

ВО = 2/3 ВМ = 2/3 СN = СО,

тогда треугольник  ВОС – равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда

∠ ОСВ = ∠ ОВС = 36°.

Так как сумма углов в треугольнике равна  180°, то

∠ ВОС = 180° – ∠ ОВС – ∠ ОСВ =

= 180° – 36° – 36° = 108°.

ЗАДАЧА:

В треугольнике  АВС:

ВN  и  СМ – медианы, АВ = 4,

О – точка пересечения  ВN  и  СМ,

∠ РВС = 35°, ∠ ВРС = 110°.
Найдите  NС.

РЕШЕНИЕ:

Так как сумма углов в треугольнике равна  180°, то

∠ РСВ = 180° – 110° – 35° =

= 35° = ∠ РВС,

значит треугольник  РВС – равнобедренный и  РВ = РС.

В треугольнике медианы точкой пересечения делятся в отношении  2 : 1, считая от вершины. Так как  РВ = РС, то 

МР = 0,5 ∙ РС = 0,5 ∙ РВ = РN.

Углы  ∠ МРВ  и  ∠ NРС – вертикальные, а значит равные.

Таким образом, треугольники  МРВ  и  РNС – равны (по двум сторонам и углу между ними), тогда

NС = МВ = 0,5 ∙ АВ = 2.

ЗАДАЧА:

В треугольнике  АВС:

ВF  и  AE – медианы, АE = BF,

О – точка пересечения  BF  и  AE,

∠ FOE = 147°.
Найдите  ∠ ABO.

РЕШЕНИЕ:

∠ АОВ = ∠ FОЕ = 147°  (как вертикальные).

В треугольнике медианы точкой пересечения делятся в отношении  2 : 1, считая от вершины. Так как  АЕ = ВF, то 

АО = 2/3 ∙ АЕ = 2/3 ∙ ВF = ВО,

тогда треугольник  АВО – равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда

∠ ОАВ = ∠ АВО.

Так как сумма углов в треугольнике равна  180°, то

180° = ∠ ОАВ +  ∠ АВО  + ∠ АОВ =

2 ∙ ∠ АБО + 147°,

откуда   ∠ АВО = 16,5°.

ЗАДАЧА:

Найдите основание равнобедренного треугольника, если угол при основании равен  30°, а взятая внутри треугольника точка находится на одинаковом расстоянии, равном  3, от боковых сторон и на расстоянии  2√͞͞͞͞͞3  от основания.
РЕШЕНИЕ:

Точка  Р  находится на равном расстоянии от обеих сторон треугольника, следовательно, лежит на биссектрисе  ВН, а так как  АВ = ВС, то  ВН  тоже является медианой и высотой.

∠ АВС = 120°, значит  ∠ АВН = ∠ КВР = 60°.

∆ КВР – прямоугольный, значит  ∠ ВРК = 30°, а против угла в  30°  лежит катет в  2 раза меньше гипотенузы. Обозначим  КВ = х, тогда  ВР = 2х. Пользуясь теоремой Пифагора составим уравнение.

4х2 = х2 + 9,

находим  х.

х = √͞͞͞͞͞3, тогда

ВР = 2√͞͞͞͞͞3,

ВН = ВР + РН =

= 2√͞͞͞͞͞3 + 2√͞͞͞͞͞3 = 4√͞͞͞͞͞3.

Так как  в  ∆АВН  угол  А = 30°,

то  АВ = 2ВР = 8√͞͞͞͞͞3.

Тогда по теореме Пифагора получаем:

АН2 = АВ2 – ВН2 =

= (8√͞͞͞͞͞3)2 – (4√͞͞͞͞͞3)2 =

= 192 – 48 = 144.

АН = 12, тогда 

АС = 2АН = 24.

ЗАДАЧА:

В равнобедренном треугольнике  АВС, в котором

АВ = ВС = 30,

АС = 48.
Найдите расстояние между точкой пересечения медиан и точкой пересечения биссектрис.

РЕШЕНИЕ:

Так как треугольник  АВС  равнобедренный, то ВК – медиана, высота и биссектриса. Тогда по теореме Пифагора:
По свойству медиан точка  М  делит медианы в отношении  2 : 1, считая от вершины, тогда 

ВМ = 12, МК = 6.

По свойству биссектрис  АТ  делит отрезок  ВМ  на части, пропорциональные прилежащим сторонам, то есть:По свойству медиан точка  М  делит медианы в отношении  2 : 1, считая от вершины, тогда 

ВМ = 12, МК = 6.

По свойству биссектрис  АТ  делит отрезок  ВМ  на части, пропорциональные прилежащим сторонам, то есть:
ТК = 8,

ТМ = ТК – КМ =

= 8 – 6 = 2.

Для прямоугольного равнобедренного треугольника

ЗАДАЧА:

В треугольнике  АВС:

∠ С = 90°,

СЕ – медиана,

∠ АСЕ = 50°.
Найдите  ∠ В.

РЕШЕНИЕ:

∠ ЕСВ = ∠ АСВ – ∠ АСЕ = 40°.

В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузе. Тогда  СЕ = ВЕ, значит треугольник  СЕВ – равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда

∠ В = ∠ ЕСВ = 40°.

ЗАДАЧА:

В прямоугольном треугольнике острый угол равен  60°. Катет, лежащий против этого угла равен  12 см.

Найдите биссектрису этого угла.

РЕШЕНИЕ:

Начертим чертёж.
Биссектриса угла в  60°  делит его на два угла по  30°. Тогда треугольник  АВL – равнобедренный. Обозначив неизвестную биссектрису за  х, получаем: 

АL = ВL = х. Тогда

СL = ВС – ВL = 12 – х.

Но  СL – катет в треугольнике  АВL, лежащий против угла  30°  и он равен половине гипотенузы, то есть 

АL = 2СL.

Находим  х.

х = 2СL = 2(12 – х),

х = 24 – 2х,

3х = 24,

х = 8.

ЗАДАЧА:

Дан прямоугольный треугольник  АВС. Из вершины  А  к стороне  ВС  проведены медиана  АD  и биссектриса  АМ. Угол между медианой и биссектрисой равен  17°.
Найдите острые углы треугольника.

РЕШЕНИЕ:

Поскольку  АМ – биссектриса, то угол  ВАМ  равен углу  МАС  и они равны  45°. Но угол  DАМ  равен  17°. Отсюда, угол  ВАD  равен разности углов  ВАМ  и  DАМ:

45° – 17° = 28°.

Мы знаем, что медиана, проведённая из вершины прямого угла прямоугольного треугольника, делит этот треугольник на два равнобедренных  треугольника. А именно треугольники  АВD  и  АDС. И теперь, поскольку треугольник  АВD  равнобедренный, то углы при основании у него равны, то есть угол  ВАD  равен углу  АВD  и они оба равны  28°. А это значит, что в прямоугольном треугольнике угол  В  равен  28°. Отсюда, угол  С  будет равен

90° – 28° = 62°.

Для равностороннего треугольника
Любая биссектриса равностороннего треугольника будет его медианой и высотой.

ЗАДАЧА:

В треугольнике  АВС:

АВ = ВС = АС = 2√͞͞͞͞͞3.
Найдите высоту  СН.

РЕШЕНИЕ:

Так как  АС = ВС, то  СН  также является медианой, следовательно,

АН = 0,5 АВ = √͞͞͞͞͞3.

Тогда по теореме Пифагора из треугольника  АСН  находим  СН:
ЗАДАЧА:
В равностороннем треугольнике  АВС, высота  СН = 2√͞͞͞͞͞3.
Найдите основание  АВ.

РЕШЕНИЕ:

Так как  АС = ВС, то  СН  также является медианой, следовательно,

АН = а, то  АВ = АС = 2а.

Тогда по теореме Пифагора из треугольника  АСН  находим  АВ:

АС2 = АН2 + СН2,

4а2 = а2 + 12,

а = 2, АВ = 2а = 4.

Задания к уроку 11
Другие уроки:
Автор: на

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)