понедельник, 16 марта 2015 г.

Урок 23. Ромб

ВИДЕОУРОК
Ромб – параллелограмм, у которого все стороны равны.

ABCD – ромб, 

AB = BC = CD = AD.
Поскольку ромб – это параллелограмм, то он имеет все свойства параллелограмма, а так же свойства, характерные только для него.

Свойства ромба.

 – диагонали ромба взаимно перпендикулярны;
– диагонали ромба являются биссектрисами углов ромба.

Признаки ромба.

 – параллелограмм, диагонали которого взаимно перпендикулярны будет ромбом; 
– параллелограмм, диагонали которого – биссектрисы его углов, будет ромбом.

ЗАДАЧА:

Угол между высотой ромба, опущенной из вершины тупого угла, и его стороной равен  25°. Найдите меньший из углов ромба.
РЕШЕНИЕ:

Из  ∆ АКВ (∠ К = 90°):

∠ А = 90° – 25° = 65°.

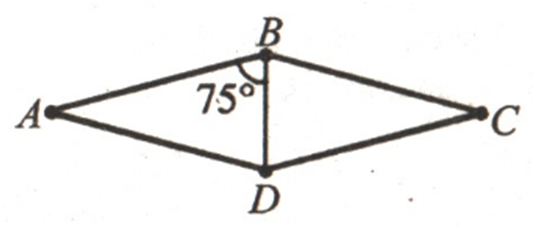
ЗАДАЧА:

У ромба  АВСD  угол  АВD  равен  75°. Найдите угол  ВСD.
РЕШЕНИЕ:

∠ ABC = 2∠ ABD =

= 2 ∙ 75° = 150°,

∠ BCD = 180° – 150° = 30°.

ЗАДАЧА:

Один из углов ромба равен  60°. Найдите меньшую диагональ ромба, если его сторона равна  15 см.

РЕШЕНИЕ:

Начертим чертёж.
∆ АВD – равнобедренный с углом  60°  при вершине, поэтому – ∆ АВD  равносторонний,

ВD = АD = 15 см.

ЗАДАЧА:

У ромба  АВСD  угол  А  равен  120°. Укажите вид треугольника  АВС.
РЕШЕНИЕ:

АС – биссектриса угла  А, поэтому

∠ САВ = 120° : 2 = 60°,

АВ = ВС,

поэтому треугольник  АВС – равнобедренный.

Так как,

∠ АСВ = ∠ САВ = 60°,

поэтому треугольник  АВС – равносторонний

ЗАДАЧА:

Сторона ромба равна  5 см, а диагональ – 8 см. Найдите другую диагональ ромба.
РЕШЕНИЕ:
Из  ∆ АОВ:
АС = 2АО = 2 ∙ 3 = 6 (см).

ЗАДАЧА:

Найдите углы ромба, если основание перпендикуляра, опущенного из вершины тупого угла, делит сторону ромба пополам.

РЕШЕНИЕ:

Из условия задачи имеем:

АВСD – ромб.

АВ = ВС = СD = DА.
ВК ⊥ АD, АК = DК.

Надо найти углы ромба.

Проведём диагональ ромба  ВD.
∆ АВD – равнобедренный с основанием  ВD,

∆ АВD – равнобедренный с основанием  АD,

значит  ∆ АВD – равносторонний.

∠ А = 60°,

∠ А = ∠ С = 60°,

∠ В = ∠ D = 120°.

ЗАДАЧА:

Какая фигура получится, если последовательно соединить середины сторон ромба ?

РЕШЕНИЕ:

Стороны полученного четырёхугольника являются средними линиями треугольников, сторонами которых являются диагонали и стороны ромба, а поэтому они параллельны диагоналям. Диагонали ромба взаимно перпендикулярны, поэтому и смежные стороны полученного четырёхугольника тоже; поэтому построенный четырёхугольник будет прямоугольником.
ЗАДАЧА:

Найдите неизвестный угол ромба.
РЕШЕНИЕ:

∠ АСК = 40° (противоположные углы ромба равны).

 ∆ АСК – равнобедренный (стороны ромба равны).

Поэтому углы при основании  АК  равны. Так как сумма углов треугольника равна  180°, то:

х + х + 40° = 180°.

Тогда  х = 70°.

ОТВЕТ:  70° 

 Задания к уроку 23
Другие уроки:
Автор: на

1 комментарий:

  1. Unknown1 марта 2021 г. в 22:15

    Великолепные задания! Блеск! Но где Решения? Или хотя бы Ответы? Чтобы "бабушки" могли подготовится, а потом уверенно давать задание внукам.
    Где "настоящая" Главная страница: с рассказом об авторе, Контактами, описанием структуры сайта?
    С уважением, Н.Н.

    ОтветитьУдалить

Подписаться на: Комментарии к сообщению (Atom)