Урок 14. Треугольник и окружность

воскресенье, 11 ноября 2018 г.

Урок 14. Треугольник и окружность

ВИДЕОУРОК

Описанная окружность разностороннего треугольника.

Окружность называется описанной около треугольника, если она проходит через все вершины этого треугольника.

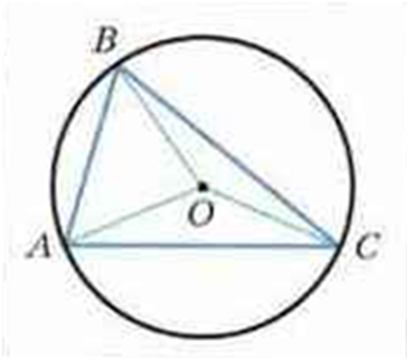
На рисунке изображена окружность, описанная около треугольника.

В этом случае также говорят, что треугольник вписан в окружность. Центр описанной окружности треугольника равноудалён от всех его вершин.

На рисунке точка О – центр окружности, описанной около треугольника АВС, поэтому

ОА = ОВ = ОС.

У остроугольного треугольника центр описанной окружности лежит внутри треугольника.

У тупоугольного треугольника центр описанной окружности лежит вне треугольника.

Около любого треугольника можно описать окружность, и притом только одну.

Серединный перпендикуляр к отрезку – прямая, проходящая через середину отрезка и перпендикулярная к нему.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.

Три серединных перпендикуляра сторон треугольника пересекаются в одной точке.

Центр окружности, описанной около треугольника, это точка пересечения серединных перпендикуляров его сторон.

Через какие-нибудь три точки, которые не лежат на одной прямой, можно провести окружность и лишь одну.

Радиус описанной вокруг треугольника окружности вычисляется по формуле:

ЗАДАЧА:

Угол С треугольника АВС, вписанного в окружность радиуса 47, равен 30°. Найдите сторону АВ этого треугольника.
РЕШЕНИЕ:

Сделаем дополнительное построение. Начертим треугольник АОВ у которого вершина О совпадает с центром окружности.
Треугольник АОВ – равносторонний, так как центральный угол АОВ равен 60° (он также соответствующий для вписанного угла, равного 30°) и тогда

АО = ОВ = АВ, а

АО и ОВ – радиусы,

значит АВ = 47.

Вписанная окружность разностороннего треугольника.

Окружность называется вписанной в треугольник, если она касается всех трёх сторон треугольника.

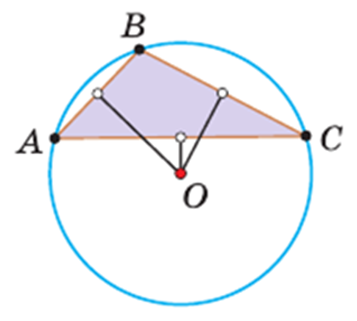
На рисунке изображена окружность, вписанная в треугольник.

В этом случае также говорят, что треугольник описан около окружности.

Точка О – центр вписанной окружности треугольника АВС, отрезки ОМ, ОN, ОР – радиусы, проведённые в точки касания,

ОМ ⊥ АВ, ОN ⊥ ВС, ОР ⊥ АС.

Поскольку ОМ = ОN = ОР, то центр вписанной окружности треугольника равноудалён от всех его сторон.

В любой треугольник можно вписать окружность, и притом только одну.

Центр окружности, вписанной в треугольник, лежит во внутренней области этого треугольника.

Центр окружности, вписанной в треугольник, – это точка пересечения его биссектрис.

В каждом треугольнике все три биссектрисы пересекаются в одной точке.

Радиус вписанной в треугольник окружности вычисляется по формуле:

ЗАДАЧА:

К окружности, вписанной в треугольник АВС, проведены три касательные, параллельные сторонам треугольника. Периметры отсечённых треугольников равны 5, 6 и 7. Найдите периметр треугольника АВС.

РЕШЕНИЕ:

Рассмотрим рисунок. Пусть А₁, В₁ С₁ – точки касания сторон ∆ АВС с окружностью. А', В', С' – точки на окружности, через которые проведены касательные параллельно сторонам треугольника. Получились треугольники AMN, BLK, CPR.
Пусть

P_AMN = 5, P_BLK= 6, P_CPR = 7.

Так как отрезки касательных, проведённых из одной точки к окружности, равны, то

МА' = МС₁, NА' = NВ₁.

Следовательно,

P_AMN = AM + МА' + NА' + AN
= AM +М С₁ + NВ₁ + AN =
АС₁ + АВ₁ = 5.

Аналогично для других треугольников:

P_BLK= ВС₁ + ВА₁ = 6

P_CPR = СА₁ + СВ₁ = 7

Следовательно,

P_A_ВС = (АС₁ + АВ₁) + (ВС₁ + ВА₁) + (СА₁ + СВ₁)

= 5 + 6 + 7 = 18.

Задания к уроку 14

Другие уроки:

Уроки математики и физики для школьников и родителей

воскресенье, 11 ноября 2018 г.