ВИДЕОУРОК
Два луча с общим началом делят плоскость на две части.
Углом называется фигура, образованная двумя отрезками, выходящими из одной точки.
Отрезки, образующие угол, называются сторонами угла, а точка, из которой они выходят – вершиной угла.
Коротко записывают:
∠ АОВ, (∠ ВОА).
Если угол обозначен тремя буквами, то средняя буква в его названии обозначает вершину угла.
Данный угол можно обозначить лишь названием его вершины, например:
∠ О
Угол также обозначают маленькими буквами греческого алфавита: α, β, γ тогда знак угла не пишут. Можно обозначать угол цифрами:
∠ 1, ∠ 2, ∠ 3.
Плоскость делится сторонами угла на внутреннюю область угла и внешнюю.
Два угла называются равными, если при наложении они совмещаются.
Если стороны углов образованы отрезками, то при равенстве углов равенство сторон может не сохраняться.
На прямой DС обозначим точку О. получилось два луча – ОС и ОD. Эти лучи выходят из общего начала О, поэтому тоже образуют угол – ∠ DОС. Такой угол называется развёрнутым.Развёрнутым углом называется такой, одна сторона которого является продолжением другой.
Два угла, которые имеют общую вершину и общую сторону, называются прилегающими, если их внутренние области не перекрывают одна одну.
При пересечении двух прямых образуются 4 угла, каждый из которые меньше чем развёрнутый. Меньший из углов, образованных при пересечении двух прямых, называют углом между двумя прямыми.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов есть дополнительными полупрямыми одной прямой.
Когда два угла равны, то смежные с ним углы тоже равны. Если угол не развёрнутый, то его градусная мера меньше, чем 180°.
На рисунке
∠ 1 и ∠ 2,
∠ 1 и ∠ 4,
∠ 2 и ∠ 3,
∠ 3 и ∠ 4
– смежные углы.
∠ 1 и ∠ 2,
∠ 1 и ∠ 4,
∠ 2 и ∠ 3,
∠ 3 и ∠ 4
– смежные углы.
Сумма смежных углов равна 180°. Чтобы построить угол, смежный с данным углом, необходимо одну из сторон данного угла продолжить за его вершину.
– если один из смежных углов острый, то другой тупой;
– если один из смежных углов острый, то другой тупой;
– если один из смежных углов тупой, то второй острый;
– если два смежных углов равны, то они прямые;
– если два угла равны, то смежные с ним углы тоже равны.
Два угла называются вертикальными, если стороны одного угла будут дополнительными полупрямыми сторон другого.
Вертикальные углы образуются при пересечению двух прямых. На рисунке
∠ 1 и ∠ 3,
∠ 2 и ∠ 4 –
вертикальные углы. Вертикальные углы равны.
∠ 1 и ∠ 3,
∠ 2 и ∠ 4 –
вертикальные углы. Вертикальные углы равны.
Биссектрисою угла называют луч, который выходит из вершины угла, проходит между его сторонами и делит угол пополам.
Каждая точка биссектрисы неразвёрнутого угла равноудалена от прямых, содержащих стороны угла.
Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе. Биссектрисы смежных углов образуют прямой угол. Геометрическим местом точек угла, равноудалённых от его сторон, будет биссектриса этого угла.
Пары углов, которые получаются в результате пересечения прямых другой прямой, которая называется секущей, имеют специальные названия.
Секущая АС составляет с прямыми АВ и СD две пары внутренних односторонних и две пары внутренних разносторонних углов. А также две пары внешних односторонних и две пары внешних разносторонних углов.
Если вершину и сторону одного угла совместить с вершиной и стороною второго так, чтобы их внутренние области не накладывались, то полученный не совмещёнными сторонами угол называется суммой данных углов.
Сумма нескольких углов определяется аналогично.
Углы измеряются:
в радианах
(1 радиан ≈ 57°18′);
Основные свойства измерения углов.
ЗАДАЧА:
Если точки В и D лежат в одной полуплоскости относительно прямой АС, то углы ВАС и DСА называются внутренними односторонними.
Секущая АС составляет с прямыми АВ и СD две пары внутренних односторонних и две пары внутренних разносторонних углов. А также две пары внешних односторонних и две пары внешних разносторонних углов.
– если внутренние разносторонние углы одной пары равны между собой, то внутренние разносторонние углы второй пары тоже равны между собой;
– если внутренние разносторонние углы равны, то сумма внутренних односторонних углов равна 180°;
– если сумма внутренних односторонних углов равна 180°, то внутренние разносторонние углы равны.
Действия с углами.
Если вершину и сторону одного угла совместить с вершиною и стороною второго, а другие стороны этих углов разместить с одной стороны от совмещённой, то:
– первый угол меньше чем второй, если не совмещённая сторона его находится в середине (во внутренней области) второго угла;
– первый угол больше чем второй, если не совмещённая сторона его находится во внешней области второго угла.
Если вершину и сторону одного угла совместить с вершиной и стороною второго так, чтобы их внутренние области не накладывались, то полученный не совмещёнными сторонами угол называется суммой данных углов.
Сумма нескольких углов определяется аналогично.
Измерение углов.
Отрезок характеризует его длина. Так само угол характеризуется своей мерой. Угол, как и всякая другая величина, может быть больше или меньше. Поэтому возникает вопрос об измерении углов.
Мерой угла служит величина поворота луча ОА вокруг точки О как центра вращения.
Полным углом называется угол, полученный при одном полном обороте луча ОА. Точка А при этом опишет окружность радиуса ОА. Половина полного угла составляет развёрнутый угол. Четвертая часть полного угла составляет прямой угол.
Измерить угол – значит сравнить его с углом, принятым за единицу измерения. За единицу измерения углов принимают угловой градус. Это есть угол, равный 1/90 части прямого угла. Представление о прямом угле получить очень просто. Надо взять лист бумаги произвольной формы и перегнуть его по прямой линии; затем этот сложенный вдвое лист перегнуть ещё раз, совместив между собой две ранее согнутые линии. Между согнутыми линиями и получился прямой угол.
Угловой градус делится на 60 равных частей, называемых минутами.
Градус обозначается маленьким нулём, поставленным около числа сверху справа. Например, если нужно обозначить, что угол имеет 30 градусов, то пишут 30°. Минута обозначается штрихом ('). Например, угол, имеющий 25 градусов 30 минут, записывают так:
25°30′.
25°30′.
Один радиан – это такой центральный угол, дуга которого равна радиусу окружности.
Обозначают радиан сокрощённо – рад. Поворот луча ОА на 1 рад – это такой поворот, при котором точка А описывает дугу, равную по длине отрезку ОА. Следовательно, в полном обороте 2π радианов. Развёрнутый угол содержит π = 3,14159… рад, а прямой угол содержит π/2 рад.
Широко распространена также градусная система измерения углов.
Чтобы измерять угол, необходимо выбрать единицу измерения – единичный угол. Часто это делают так. Развёрнутый угол делят на 180 равных частей и одну из них принимают за единичный угол. Его меру называют градусом. Для каждого угла можно определить его градусную меру. На практике для сравнения углов, как и отрезков, можно пользоваться способом наложения. Равные углы имеют равные градусные мери. Из двух углов большим будет тот, градусная мера которого больше. Градусная мера угла равна сумме градусных мер его частей.
Есть такие единицы измерения углов:
– 1 градус. В переводе с латинского gradus означает ступень, шаг. Записывают 1° – это угол, который составляет 1/360 часть полого угла. Дуга центрального угла 1° составляет 1/360 часть окружности.
– 1 минута – это 1/60 часть градуса. Записывают 1′;
– 1 секунда – это 1/60 часть минуты. Записывают 1′′.
Слово ’’минута’’ от латинского minutes – уменьшенный, маленький, – что в данном случае означает меньшую часть градуса, а слово ’’секунда’’ происходит от латинского secunda – другой, то есть второй (меньший) раздел градуса.
ПРИМЕР:
Угол 40 градусов 37 минут и 15 секунд записывают так:
40°37′15′′.
В полном обороте 360°, что эквивалентно 2π рад.
Переход от градусного измерения до радианного и наоборот вычисляется по формулам:Углы измеряются:
в радианах
(1 радиан ≈ 57°18′);
в градах
(1 град ≈ 0,9°);
(1 град ≈ 0,9°);
в румбах
(1 румб ≈ 11,29°).
(1 румб ≈ 11,29°).
Для измерения и построения углов служит прибор, называемый транспортиром. Он состоит из линейки, к которой прикреплена полуокружность. Центр полуокружности отмечен штрихом или небольшим углублением на диаметре. Дуга полуокружности разделена на градусы от 0° до 180°. Чтобы при помощи транспортира измерить угол, поступают следующим образом. Прикладывают линейку транспортира к одной из сторон угла так, чтобы вершина угла совпала с центром транспортира. Тогда вторая сторона угла пересечёт окружность транспортира в какой – нибудь точке. Число, стоящее в этой точке дуги транспортира, и укажет, сколько градусов имеет измеряемый угол. Если, например, сторона угла прошла через 40 – е деление, то, значит, измеряемый угол равен 40°.
Развёрнутый угол содержит 180°. Углы, меньше от развёрнутого, можно поделить на три вида – прямые, острые или тупые углы. Угол, который равен 90°, называют прямым. Угол, меньше 90°, называют острым, а больше 90° – тупым.Основные свойства измерения углов.
1. Каждый угол имеет определённую градусную меру, большую от нуля. Развёрнутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на который они разбиваются какой-нибудь прямой, которая выходит из его вершины и проходит между сторонами угла.
2. От любой полупрямой в данной полуплоскости можно отложить угол с данной градусной мерой, меньшей чем 180°, и только один.
Фигура симметрична относительно прямой, если для каждой точки фигуры симметричная ей точка относительно прямой также принадлежит этой фигуре. Прямая – ось симметрии фигуры, а фигура обладает осевой симметрией.
Фигура, обладающая осевой симметрией – это неразвёрнутый угол,
который имеет одну ось симметрии – прямую на которой расположена биссектриса угла.
Задачи на построение.
ЗАДАЧА:
При вершине N на луче NM построить угол, который равен данному ∠ АВС.
Из вершины B описываем дугу pq произвольного радиуса и тем же самым радиусом из центра N проведём дугу, которая пересекает луч NM в точке Р. Из точки Р радиусом, который равен отрезку pq, делаем засечку и полученную точку Q соединяем с вершиной N.
Угол QNM – искомый.
Угол QNM – искомый.
ЗАДАЧА:
Построить углы, которые равны 30°, 60° и 90°.
Из концов А и В произвольного отрезка АВ как из центров описываем радиусом R = АВ две дуги. Точки их пересечения С и D соединяем прямой, которая пересекает отрезок АВ в его середине О. Точку А соединяем прямой с точкой С. Тогда
∠ АСО = 30°,
∠ САО = 60°,
∠ АОС = 90°.
Данный ∠ ВАС поделить пополам.
Из вершины А произвольным радиусом проводим дугу DЕ. Из точек D и Е пересечения со сторонами АВ і АС описываем произвольными равными радиусами дуги аb, сd. Точку их пересечения F соединяем с А; полученная прямая АF делит ∠ ВАС пополам, т. е. является его биссектрисой.
ЗАДАЧА:
Разделить прямой угол на три равные части.
Произвольным радиусом проводим дугу с центром в вершине А данного угла до её пересечения в точках М и N с его сторонами. Этим же радиусом из точек М и N как из центров, на дуге МN делаем две засечки K и L, которые соединяем с вершиной А.
∠ MAK = ∠ KAL
= ∠ LAN = 30°.ЗАДАЧА:
Разделить данный угол BAC на три равные части.
С помощью линейки без делений и циркуля точно выполнить это построение, которое называют трисекцией угла, нельзя. Однако с помощью циркуля и меченой линейки (т. е. линейки, с нанесённой на неё равномерной шкалой, например миллиметровой) трисекцию угла легко выполнить следующим образом. Произвольным радиусом АС описываем из вершины угла A окружность. Продолжаем АС за точку А. Кладем меченую линейку так, чтобы она проходила через В, и вращаем её вокруг В, до тех пор пока отрезок ЕD между окружностью и прямой АК не станет равным радиусу АС. Тогда ∠ EDF есть треть угла BAC . Это легко доказать, пользуясь тем, что, согласно построения ∆DEA равнобедренный, а тогда по теореме о внешнем угле треугольника
∠ BEA = 2x;
∠ BAC = α = x + 2x,
x = ∠ EDA.
Задания к уроку 2
Другие уроки:
- Урок 1. Точка и прямая
- Урок 3. Параллельные и перпендикулярные прямые
- Урок 4. Окружность
- Урок 5. Угол и окружность
- Урок 6. Треугольник (1)
- Урок 7. Треугольник (2)
- Урок 8. Прямоугольный треугольник (1)
- Урок 9. Прямоугольный треугольник (2)
- Урок 10. Равнобедренный треугольник (1)
- Урок 11. Равнобедренный треугольник (2)
- Урок 12. Периметр треугольника
- Урок 13. Периметр равнобедренного (равностороннего) треугольника
- Урок 14. Треугольник и окружность
- Урок 15. Прямоугольный треугольник и окружность
- Урок 16. Равнобедренный треугольник и окружность
- Урок 17. Четырёхугольники
- Урок 18. Параллелограмм
- Урок 19. Периметр параллелограмма
- Урок 20. Прямоугольник
- Урок 21. Периметр прямоугольника
- Урок 22. Квадрат
- Урок 23. Ромб
- Урок 24. Периметр ромба
- Урок 25. Трапеция
- Урок 26. Равнобедренная трапеция
- Урок 27. Периметр трапеции
- Урок 28. Четырёхугольник и окружность (1)
- Урок 29. Четырёхугольник и окружность (2)
- Урок 30. Многоугольник
- Урок 31. Правильный многоугольник
- Урок 32. Осевая и центральная симметрии






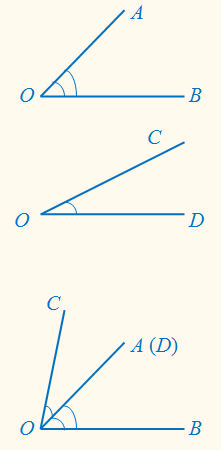







Комментариев нет:
Отправить комментарий