Урок 20. Прямоугольник

понедельник, 26 ноября 2018 г.

Урок 20. Прямоугольник

ВИДЕОУРОК

Среди четырёхугольников особое место занимает прямоугольник.

Прямоугольник – параллелограмм, у которого все углы прямые, а диагонали равны.

ABCD – прямоугольник,

∠ A = ∠ B = ∠ C = ∠ D = 90°.

Прямоугольник вместе с частью плоскости, которую он ограничивает, называется плоским прямоугольником. У него 4 вершины, 4 стороны и 4 угла. Все углы прямоугольника – прямые, противоположные стороны – попарно равны, но смежные стороны (длина и ширина) имеют разные длины. Прямоугольник – отдельный вид параллелограмма, поэтому он имеет все свойства параллелограмма. У прямоугольника:

– противоположные стороны равны;
– противоположные углы равны;
– диагональ делить его на два равных треугольника;
– диагонали точкою пересечения делятся пополам;
– диагонали прямоугольника равны;
– сумма углов, прилегающих к одной стороне, равна 180°.

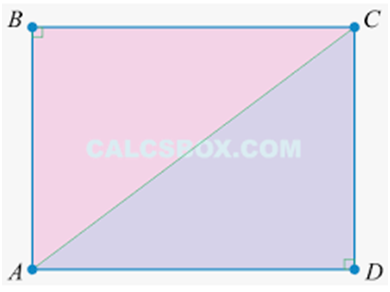
Если диагонали в параллелограмме равны, то этот параллелограмм – прямоугольник.Построить прямоугольник можно следующим образом.

Построим прямоугольник АВСD, у которого

АD = 6 см,

АВ = 4 см.

Начертим прямую ЕF и отложим на ней отрезок АD длиной 6 см.

С помощью угольника построим с одной стороны от прямой ЕF прямые углы NАF и МDF. Отложим на луче АN отрезок АВ длиной 4 см и на луче DМ – отрезок DС, равный 4 см. Соединив точки В и С отрезком, получим искомый прямоугольник АВСD.

ЗАДАЧА:

Какая часть прямоугольника закрашена на рисунку ?

РЕШЕНИЕ:

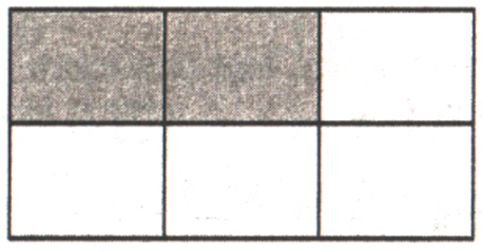
Закрашено 2 из 6 одинаковых прямоугольников, то есть

²/₆ = ¹/₃ часть.

ЗАДАЧА:

О – точка пересечения диагоналей прямоугольника АВСD,

∠ СОD = 52°.
Найдите ∠ DВС.

РЕШЕНИЕ:

∠ ОВС =∠ ОСВ,

∠ СОD = ∠ ОВС +∠ ОСВ =

= 2∠ ОВС,

∠ DВС =∠ ОВС =∠ СОD : 2 =

= 52° : 2 = 26°.

ЗАДАЧА:

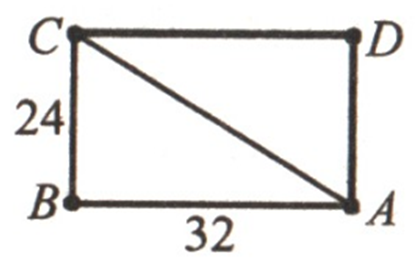
Стороны прямоугольника равны 32 см и 24 см. Найдите длину диагонали прямоугольника.

РЕШЕНИЕ:

Начертим чертёж.

По теореме Пифагора
ЗАДАЧА:

Сторона прямоугольника равна 4 см и образует с диагональю угол 60°. Найдите эту диагональ.

РЕШЕНИЕ:

Из условия задачи имеем:

АВСD – прямоугольник,

ВС = 4 см, ∠ ВСА = 60°.

Найдите АС.

∆ АВС – прямоугольный, в нём катет

ВС = 4 см, а ∠ ВАС = 30°.

По свойству катета, лежащего в прямоугольном треугольнике против угла 30°,

ВС = 0,5АС.

Значит АС = 8 см.

ЗАДАЧА:

Дано: АВСD – прямоугольник, АВ = ВЕ.

Найти: ∠ ВАЕ.
ВС = 4 см, ∠ ВСА = 60°.

Найдите АС.

∆ АВС – прямоугольный, в нём катет

ВС = 4 см, а ∠ ВАС = 30°.

По свойству катета, лежащего в прямоугольном треугольнике против угла 30°,

ВС = 0,5АС.

Значит АС = 8 см.

ЗАДАЧА:

Дано: АВСD – прямоугольник, АВ = ВЕ.

Найти: ∠ ВАЕ.
РЕШЕНИЕ:

В ∆ АВЕ ∠ В = 90° (как один из углов прямоугольника).

АВ = ВЕ, поэтому

∆ АВЕ – равнобедренный с основанием АЕ.

∠ А = ∠ Е как углы при основании равнобедренного треугольника, в сумме они составляют 90° как острые углы прямоугольного треугольника. Значить,

∠ А = ∠ Е = 45°,

∠ ВАЕ = 45°.

ОТВЕТ: 45°.

ЗАДАЧА:

Диагональ делит угол прямоугольника в отношении 1 : 2, а меньшая сторона равна 12 см. Найдите диагональ прямоугольника.

РЕШЕНИЕ:

Пусть ЕКРМ – данный прямоугольник у которого

∠ РЕК : ∠ РЕМ = 2 : 1.

∠ КЕМ = 90° (как угол прямоугольника).

Обозначим через k коэффициент пропорциональности, тогда

∠ РЕК = 2k, а

∠ РЕМ = k.

Поэтому,

2k + k = 90°.

Откуда

∠ РЕК = 60°, а

∠ РЕМ = 30°.

Рассмотрим

∆ РЕМ (∠ М = 90°).

РМ = ¹/₂ЕР (как катет противоположный углу в 30°).

Значит

ЕР = 2 РМ = 24 см.

ЗАДАЧА:

В равнобедренный прямоугольный треугольник вписан прямоугольник так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Чему равны стороны прямоугольника, если известно, что они относятся как 5 : 2, а гипотенуза треугольника равна 45 см

РЕШЕНИЕ:

∆ АВС – равнобедренный, отсюда

∠ А = ∠ С =
¹/₂ (180° – 90°) = 45°.

∆ АFК и ∆ СEL – равнобедренные, так как

∠ АКF = 180° – ∠ F – ∠ А =

180° – 90° – 45° = ∠ А

и аналогично ∠ ЕLК = ∠ С.

Поэтому

АF = FК и LE = ЕС.

К тому же КF = LE (стороны прямоугольника), так что

АF = КF = LЕ = ЕС.

Пусть FК = 2х, а КL = 5х.

Тогда АF = ЕС = FК = 2х

и FЕ = КL = 5х.

Получим
АС = АF + FЕ + EС =
2х + 5х + 2х = 9х = 45,

откуда х = 5.

Далее,

FК = 2х = 10 см,

КL = 5х = 25 см.

ОТВЕТ: 10 см, 25 см.

ЗАДАЧА:

Биссектриса угла А прямоугольника АВСD делить его сторону ВС на отрезки ВМ и МС длиной 10 см и 14 см соответственно. На отрезки какой длины эта биссектриса делит диагональ прямоугольника ?

РЕШЕНИЕ:

Пусть АВСD – заданный прямоугольник,
АМ – биссектриса угла А,

ВМ = 10 см,

МС = 14 см.

Тогда ВС = 24 см.

Поскольку АМ – биссектриса угла, то

∠ 1 = ∠2.

∠ 1 = ∠ 3

как внутренние разносторонние для параллельных прямых ВС и АD и секущей АМ.

Получим:

∠ 2 = ∠ 3.

Поэтому, треугольник АВМ – равнобедренный,

АВ = ВМ = 10 см.

З ∆ ВАD (∠ А = 90°):

О – точка пересечения биссектрисы АМ и диагонали ВD.

Пусть ВО = х, тогда

ОD = 26 – х.

По свойству биссектрисы

АС ∆ АВD:

12х = 130 – 5х,

17х = 130, х = ¹³⁰/₁₇.

Поэтому,

ВО = ¹³⁰/₁₇ = 7¹¹/₁₇ (см).

ОD = 26 – 7¹¹/₁₇ = 18⁶/₁₇ (см)

ОТВЕТ:

7¹¹/₁₇ см, 18⁶/₁₇ см

ЗАДАЧА:

Биссектриса угла прямоугольника делит диагональ на отрезки длиной 30 см и 40 см. На отрезки какой длины делит эта биссектриса сторону прямоугольника ?

РЕШЕНИЕ:

Пусть АВСD – заданный прямоугольник,
АМ – биссектриса угла А, которая пересекает диагональ ВD в точке О,

ВО = 30 см,

ОD = 40 см.

Тоді ВD = 30 + 40 (см).

Так как АМ – биссектриса угла, то

∠ 1 = ∠2,

∠ 1 = ∠ 3

как внутренние разносторонние для параллельных прямых ВС и АD и секущей АМ.

Получим:

∠ 2 = ∠ 3.

Поэтому, треугольник АВМ – равнобедренный,

АВ = ВМ.

По свойству биссектрисы угла А в треугольнику ВАD получим:

Откуда

АВ = 3х, АD = 4х.

Из ∆ ВАD (∠ А = 90°):

АВ² + АD² = ВD²,

9х² + 16х² = 4900,

25х² = 4900, х = 14.

Поэтому,

АВ = 3 ∙ 14 = 42 (см).

АD = 4 ∙ 14 = 56 (см).

Так как

АВ = ВМ, то

ВМ = 42 см,

МС = ВС – ВМ =

= 56 – 42 = 14 (см).

ОТВЕТ: 42 см, 14 см

Задания к уроку 20

Другие уроки:

Уроки математики и физики для школьников и родителей

понедельник, 26 ноября 2018 г.