Уроки математики и физики (RU + UA)

▼

четверг, 2 апреля 2015 г.

Урок 21. Периметр прямоугольника

ВИДЕОУРОК

Периметр прямоугольника.

На практике очень часто приходится решать задачи по определению периметра прямоугольника.

Прямоугольник  – это фигура, лежащая в одной плоскости. Если мы измерим и сложим все стороны прямоугольника, то получим число, которое называется периметром данного прямоугольника. Если в прямоугольнике обозначим одну из сторон  а, а вторую  b, то периметр прямоугольника  Р  будет равен:
Найти периметр прямоугольника – это значит вычислить сумму его сторон. Если периметр – это сумма длин всех сторон фигуры, то полупериметр – сумма одной длины и одной ширины.

ЗАДАЧА:

Периметр прямоугольника  26 см, а одна сторона его равна  5 см. Найдите другую сторону.

РЕШЕНИЕ:

Здесь  Р = 26 см, допустим, что  а = 5 см. Подставив значения  Р  и  а  в формулу,

получим уравнение

26 = 2(5 + b).

Решим его:

2(5 + b) = 26,

5 + b = 26 : 2, 

5 + b = 13,

b = 13 – 5, b = 8.

ЗАДАЧА:

Биссектриса угла  С  прямоугольника  АВСD  пересекает сторону  АD  в точке  К,

DК = 4 см, АК = 6 см.

Найдите периметр прямоугольника.
РЕШЕНИЕ:

∠ КСD = 90° : 2 = 45°,

З  ∆ СDК:

СD = КD = 4 (см).

Р = 2(4 + (6 + 4)) = 28 (см).

ЗАДАЧА:

В прямоугольном треугольнике через середину его гипотенузы проведены прямые, параллельные катетам. Найдите периметр образовавшегося прямоугольника, если катеты треугольника равны  10 см и  8 см.

РЕШЕНИЕ:

Начертим чертёж.
Из условия задачи имеем:

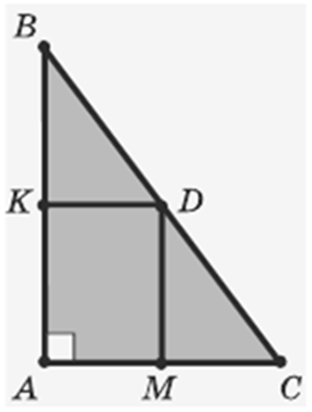
∆ АВС – прямоугольный,

∠ А – прямой,

D – середина гипотенузы.

КD ∥ АС, DМ ∥ АВ.

Катеты равны  10 см  и  8 см.

Так как 

КD = 1/2 АС = 4 см,

МD = 1/2 АВ = 5 см,

согласно свойству средней линии треугольника, то периметр прямоугольника  АКDМ  равен:

Р = 2(4 + 5) = 18 (см).

ЗАДАЧА:

Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна  10 см.

РЕШЕНИЕ:
∠ 1 = ∠ 2 (так как  АО – биссектриса).
∠ 2 = ∠ 3 (как накрест лежащие углы для прямых  ВС, АD  и секущей  АО).
Значит, ∠ 1 = ∠ 3  и  ∆ АОВ – равнобедренный. Поэтому 
АВ = ВО = 10 см (стороны равнобедренного треугольника).
ВО = ОС  (по условию). Значит, ОС = 10 см,
ВС = ВО + ОС = 
10 см + 10 см = 20 см.
РАВСВ = 2(АВ + ВС) =
2(10 см + 20 см) = 60 см.

ОТВЕТ:  60 см

ЗАДАЧА:

В прямоугольнику биссектриса одного из углов делит сторону на отрезки  20 см  и  30 см. Найдите периметр прямоугольника.

РЕШЕНИЕ:

Так как сторона прямоугольника делится на отрезки  20 см  и  30 см, то её длина – 50 см. Противоположная ей сторона также равна  50 см.

Другая сторона прямоугольника может быть как  20 см  так и  30 см. Поэтому:

а) Если другая сторона  20 см  и противоположная ей сторона  20 см, то периметр прямоугольника

20 см + 20 см + 50 см + 50 см = 140 см.

б) Если другая сторона  30 см  и противоположная ей сторона  30 см, то периметр прямоугольника

30 см + 30 см + 50 см + 50 см = 160 см.

ОТВЕТ: 

140 см  або  160 см
Задания к уроку 21
Другие уроки:
на

Комментариев нет:

Отправить комментарий