Пусть дано
уравнение с двумя переменными f(х; у)
= 0. Если все его
решения изобразить точками на координатной плоскости, то получится некоторое
множество точек плоскости. Это множество называют графиком уравнения f(х;
у) = 0.
Например,
Графиком
уравнения у
– х2 = 0 является
парабола у
= х2.
Графиком
уравнения у
– х = 0 является прямая (биссектриса первого и третьего
координатных углов).
Алгоритм построения графика уравнения аx + by = c.
– выбрать
любое удобное значение переменной х = х1
и из уравнения аx + by =
c вычислить
значение у
= у1;
– выбрать
другое значение переменной х = х2 и
из уравнения аx
+ by = c вычислить значение у = у2;
– на
координатной плоскости отметить точки (х1; у1), (х2; у2);
– через точки
провести прямую – она является искомым графиком.
ПРИМЕР:
Изобразите решения линейного уравнения
–х + у – 2 = 0
точками в координатной плоскости хОу.
РЕШЕНИЕ:
Несложно подобрать несколько решений:
(3; 5), (2; 4), (1; 3), (0; 2), (–2; 0).
–х + у – 2 = 0.
ПРИМЕР:
Начертить график уравнения
х – 2у – 4 = 0.
РЕШЕНИЕ:
Подставим х = 0 в
уравнение, получим:
0 – 2у – 4 = 0,
–2у = 4, у =
– 2.
Подставим у = 0 в
уравнение, получим:
х – 2 ∙ 0
– 4 = 0,
х – 4 = 0, х =
4.
Отметим полученные точки
(0; –2) и (4; 0) в прямоугольной
системе координат.
х – 2у – 4 = 0.
ПРИМЕР:
Построить график уравнения
2х – 3у
= –6.
РЕШЕНИЕ:
Графиком этого линейного
уравнения является прямая. Для построения прямой достаточно знать две её точки.
Подставив в уравнение
2х – 3у
= –6
вместо х значение 0, получим –3у
= –6, откуда у = 2.
Подставив в уравнение
2х – 3у
= –6
вместо у значение 0, получим 2х
= –6, откуда х = –3.
Итак, мы нашли две точки
графика:
(0; 2) и (–3; 0).
Проведя через них прямую линию,
получим график уравнения
Графиком любого линейного уравнения
аx + by = c,
у которого хотя бы один из коэффициентов при переменных отличен от нуля,
является прямая линия.
Если b = 0, то эта прямая параллельна
оси у.
Его решениями служат все пары чисел (х; у), в которых х = 4, а у – любое число, например (4; 2), (4; 0), (4; –4,5). График уравнения состоит из всех точек, абсцисса которых равна 4, а ордината – произвольному числу. Такие точки образуют прямую, проходящую через точку (4; 0) и параллельную оси у.
ПРИМЕР:
Найдите множество точек
координатной плоскости хОу, координаты х, у которых удовлетворяют уравнению:
2х2
– 8х + у2 + 6у + 17 =
0.
РЕШЕНИЕ:
Это уравнение имеет
единственное решение:
х = 2, у =
–3,
то есть данному уравнению
удовлетворяют координаты только одной точки
М(2: –3).
ПРИМЕР:
Найдите множество точек
координатной плоскости хОу, координаты х, у которых удовлетворяют уравнению:
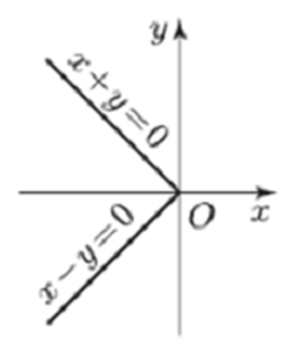
|х| = |у|.
РЕШЕНИЕ:
Уравнение равносильно совокупности уравнений
х = у и х
= –у.
Найдите множество точек
координатной плоскости хОу, координаты х, у которых удовлетворяют уравнению:
х + |у| = 0,
РЕШЕНИЕ:
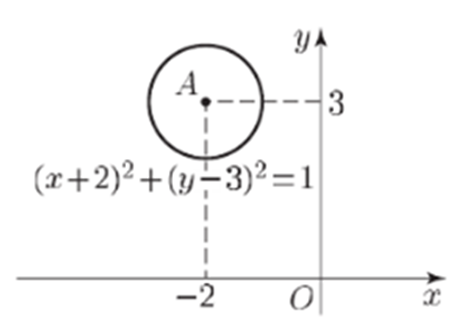
Найдите множество точек
координатной плоскости хОу, координаты х, у которых удовлетворяют уравнению:
х2 + 4х + у2
– 6у + 12 = 0.
РЕШЕНИЕ:
Запишем уравнение в виде:
(х2
+ 4х + 4) + (у2 – 6у + 9) –
1 = 0,
(х + 2)2 + (у – 3)2 = 1.
- Урок 1. Линейные уравнения с одной переменной и целыми свободными членами
- Урок 2. Линейные уравнения с одной переменной и дробными свободными членами
- Урок 3. Применение правил определения неизвестного слагаемого, уменьшаемого и вычитаемого для решения задач
- Урок 4. Применение правил определения неизвестного множителя для решения задач
- Урок 5. Решение уравнений, сводимых к линейным
- Урок 6. Решение уравнений с переменной в знаменателе
- Урок 7. Применение правил опреднления делимого и делителя для решения задач
- Урок 8. Линейные уравнения с двумя переменными
- Урок 10. Линейные уравнения с параметрами
- Урок 11. Системы уравнений первой степени с двумя неизвестными
- Урок 12. Решение систем уравнений способом подстановки
- Урок 13. Решение систем уравнений способом алгебраического сложения
- Урок 14. Решение линейных систем уравнений с помощью графиков
- Урок 15. Решение задач с помощью систем уравнений первой степени
- Урок 16. Системы линейных уравнений с тремя неизвестными
- Урок 17. Полное квадратное уравнение общего вида
- Урок 18. Приведённое квадратное уравнение
- Урок 19. Теорема Виета
- Урок 20. Неполные квадратные уравнения
- Урок 21. Решение квадратных уравнений выделением квадрата двучлена
- Урок 22. Графический способ решения квадратных уравнений
- Урок 23. Квадратный трёхчлен
- Урок 24. Квадратные уравнения с параметрами
- Урок 25. Дробные рациональные уравнения
- Урок 26. Решение задач с помощью квадратных уравнений
- Урок 27. Уравнение окружности
- Урок 28. Системы уравнений второй степени с двумя неизвестными
- Урок 29. Решение задач с помощью систем уравнений второй степени
- Урок 30. Пересечение прямой и окружности
- Урок 31. Решение нелинейных систем уравнений с помощью графиков
- Урок 32. Системы уравнений с параметрами
- Урок 33. Уравнения высших стапеней
- Урок 34. Решение уравнений способом замены
- Урок 35. Решение систем уравнений способом замены
- Урок 36. Задачи на нахождение чисел
- Урок 37. Задачи на нахождение цифр
- Урок 38. Решение задач на смешивание с помощью уравнений
- Урок 39. Решение задач на смешивание с помощью систем уравнений
- Урок 40. Иррациональные уравнения
- Урок 41. Уравнения с модулем










Комментариев нет:
Отправить комментарий