– найти общий знаменатель всех имеющихся дробей;
– заменить данное уравнение целым, умножив обе его
части на общий знаменатель;
– решить полученное целое уравнение;
– исключить из его корней те, которые обращают в нуль
общий знаменатель.
х = 0,5 – корень данного уравнения.
х2 – 6х + 8 = 0.
находим х1 = 2, х2 = 4.
Осталось проверить обращают ли найденные корни
выражение 2х(2 – х) в нуль, то есть проверить выполнение условия
2х(2 – х) ≠ 0.
Замечаем, что 2 не удовлетворяет
этому условию, а 4 удовлетворяет.
Значит, х = 4 –
единственный корень уравнения.
ПРИМЕР:
РЕШЕНИЕ:х1 = –6, х2 = 4,
х ≠ –6, х ≠ 6.
х(х – 2) = 0, если х = 0 или х = 2.
ПРИМЕР:
РЕШЕНИЕ: Решите уравнение:4х2 + х + 8х + 2 + 4х2 – х – 8х + 2 = 6х + 3,8х2 – 6х + 1 = 0,
х1 = 0,25, х2 = 0,5,
х ≠ –0,25, х ≠ 0,25.
ОТВЕТ: х = 0,5
ПРИМЕР:
РЕШЕНИЕ: Решите уравнение:2х2 – 13х + 11 = 0,х1 = 1, х2 = 5,5,
х ≠ 0, х ≠ 2.
ОТВЕТ: х1 = 1, х2 = 5,5
ПРИМЕР:
х1 = 1, х2 = –2,
х ≠ 2, х ≠ –2.
ОТВЕТ: х = 1
ПРИМЕР:
х1 = 7, х2 = –2,
х ≠ 2, х ≠ –2,
ОТВЕТ: х = 7.
ПРИМЕР:
х1 = 2, х2 = –4,
х ≠ 2, х ≠ 0.
ОТВЕТ: х = –4
ПРИМЕР:
РЕШЕНИЕ:х2 + 7х – 8 = 0,
х1 = 1, х2 = –8,
х ≠ –8, х ≠ 8.
ОТВЕТ: х = 1
ПРИМЕР:
х1 = 9, х2 = –5,
х ≠ –5, х ≠ 5.
ОТВЕТ: х = 9
ПРИМЕР:
2х2 – 5х = 0
х1 = 0, х2 = 2,5,
х ≠ 0, х ≠ 1.
ОТВЕТ: х = 2,5
ПРИМЕР:
х2 – 2х = 0,
х1 = 0, х2 = 2,
х ≠ 0, х ≠ –2.
ОТВЕТ: х = 2
ПРИМЕР:
х2 + 2х – 8 = 0,
х1 = –4, х2 = 2,
х ≠ 4, х ≠ –4.
ОТВЕТ: х = 2
ПРИМЕР:
(х + 12)2 = 0,
х = –12,
х ≠ 0, х ≠ –4, х ≠ 4.
ОТВЕТ: х = –12
ПРИМЕР:
х1 = 1, х2 = 2,
х ≠ 2, х ≠ –2.
- Урок 1. Линейные уравнения с одной переменной и целыми свободными членами
- Урок 2. Линейные уравнения с одной переменной и дробными свободными членами
- Урок 3. Применение правил определения неизвестного слагаемого, уменьшаемого и вычитаемого для решения задач
- Урок 4. Применение правил определения неизвестного множителя для решения задач
- Урок 5. Решение уравнений, сводимых к линейным
- Урок 6. Решение уравнений с переменной в знаменателе
- Урок 7. Применение правил опреднления делимого и делителя для решения задач
- Урок 8. Линейные уравнения с двумя переменными
- Урок 9. Решение линейных уравнений с помощью графиков
- Урок 10. Линейные уравнения с параметрами
- Урок 11. Системы уравнений первой степени с двумя неизвестными
- Урок 12. Решение систем уравнений способом подстановки
- Урок 13. Решение систем уравнений способом алгебраического сложения
- Урок 14. Решение линейных систем уравнений с помощью графиков
- Урок 15. Решение задач с помощью систем уравнений первой степени
- Урок 16. Системы линейных уравнений с тремя неизвестными
- Урок 17. Полное квадратное уравнение общего вида
- Урок 18. Приведённое квадратное уравнение
- Урок 19. Теорема Виета
- Урок 20. Неполные квадратные уравнения
- Урок 21. Решение квадратных уравнений выделением квадрата двучлена
- Урок 22. Графический способ решения квадратных уравнений
- Урок 23. Квадратный трёхчлен
- Урок 24. Квадратные уравнения с параметрами
- Урок 26. Решение задач с помощью квадратных уравнений
- Урок 27. Уравнение окружности
- Урок 28. Системы уравнений второй степени с двумя неизвестными
- Урок 29. Решение задач с помощью систем уравнений второй степени
- Урок 30. Пересечение прямой и окружности
- Урок 31. Решение нелинейных систем уравнений с помощью графиков
- Урок 32. Системы уравнений с параметрами
- Урок 33. Уравнения высших стапеней
- Урок 34. Решение уравнений способом замены
- Урок 35. Решение систем уравнений способом замены
- Урок 36. Задачи на нахождение чисел
- Урок 37. Задачи на нахождение цифр
- Урок 38. Решение задач на смешивание с помощью уравнений
- Урок 39. Решение задач на смешивание с помощью систем уравнений
- Урок 40. Иррациональные уравнения
- Урок 41. Уравнения с модулем































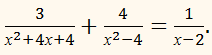

Комментариев нет:
Отправить комментарий