Квадратным уравнением (уравнение второй степени с одной переменной) называют уравнение вида:
а ≠ 0.
Коэффициенты а, b, с имеют следующие названия:
ах2 – старшим членом,
bх –
членом, который определяет первую степень неизвестного.
Если b ≠ 0, c ≠ 0,
то квадратное уравнение называют полным квадратным уравнением.
Квадратное уравнение
можно решить по формуле:
Выражение
b2 – 4ac,
которое находится в этой формуле под радикалом, называется дискриминантом квадратного уравнения общего в вида. Его обычно обозначают буквою D, а формулу корней записывают так:
– если D < 0, то данное уравнение не имеет корней: нет такого значения х, при котором значение выражения
(2ах + b)2 было б отрицательным;
– если D = 0,
– если D > 0, то данное квадратное уравнение равносильно уравнению:
откуда
или
В этом случае данное уравнение имеет два корня, которые отличаются только знаками перед значением √͞͞͞͞͞D . Коротко записывают их так:
На примерах покажем, как можно использовать общую формулу корней для решения квадратных уравнений.
ПРИМЕР:
Решите уравнение:
3х2 + 11х + 6 = 0.
а = 3, b = 11, с = 6.
72х + 6(х2 – 6х + 9)
= 3(х2 + 6х + 9) + 8(х2
– 1);
72х + 6х2
– 36х + 54
= 3х2 + 18х + 27 + 8х2 –
8;
–5х2 + 18х + 35 = 0;
Не решая уравнения, определите, сколько действительных корней оно имеет:
4х2 + 6х + 9 = 0.
РЕШЕНИЕ:
D = 62 – 4 × 4 × 9
= 36 – 144 < 0.
Уравнение не имеет действительных корней.
ПРИМЕР:
Не решая уравнения, определите, сколько действительных корней оно имеет:
2х2 – 3х + 1 = 0.
РЕШЕНИЕ:
D = (–3)2 – 4 × 2 × 1
= 9 – 8 > 0.
уравнение имеет два действительных разных корня.
ПРИМЕР:
Решите уравнение:
3х2 – 5х + 2 = 0.
х1 = 1, х2 = 2/3.
ПРИМЕР:
Решите уравнение:
5х2 – х + 1 = 0.
D =
1 – 20 = –19, D < 0,
ОТВЕТ:
Корей нет.
ПРИМЕР:
Решите уравнение:
2х2 + 5х – 1 = 0.
D = 25 – 4 ∙ 2 ∙ (–1) = 33 > 0,ОТВЕТ:
Другой вид формулы корней квадратного уравнения.
Корни квадратного уравнения:
ах2 + bx + c = 0
можно найти, как известно, по формуле;
на 2 и внесём множитель 1/2 под знак корня. Получим:
поскольку
то есть:
Формула корней квадратного уравнения приобретает вид:
Формулой, которая записана в таком виде, можно пользоваться для решения любого квадратного уравнения, дискриминант которого отрицательный. На практике, как правило, её применяют тогда, когда b – чётное число и, тогда b/2 – целое число.
ПРИМЕР:
Пусть необходимо решить уравнение:
9х2 – 14х + 5 = 0.
ПРИМЕР:
Решим уравнение:
5х2 + 8х + 6 = 0.
В этом уравнении
b/2 = 4, а = 5, с = 6.
D/4 =
42 – 5 × 6 = –14.
Мы нашли,
что D/4 – отрицательное число. Поскольку
дискриминант отрицательный, то уравнение не имеет корней.
ПРИМЕР:
Сколько корней имеет уравнение ?
54х2 – 5х – 19 = 0.
РЕШЕНИЕ:
Найдём дискриминант по формуле:
D =
b2 – 4ac =
= (–5)2 –
4 ∙ 54 ∙
(–19) =
= 25 + 4 ∙ 54 ∙
19 > 0.
Так как дискриминант больше нуля, значит,
уравнение имеет два корня.
ПРИМЕР:
Найдите сумму корней квадратного уравнения.
2х2 + 6х – 15 = 0.
РЕШЕНИЕ:
Найдём сумму корней квадратного уравнения:ПРИМЕР:
Решите уравнение:
2х2 – 5х + 2 = 0.
РЕШЕНИЕ:
ПРИМЕР:
Решите уравнение:
х2 – 6х + 9 = 0.
РЕШЕНИЕ:
Здесь
а = 1, b =
–6, с = 9.
ПРИМЕР:
Решите уравнение:
2х2 – 3х + 5 = 0.
РЕШЕНИЕ:
Здесь
а = 2, b =
–3, с = 5.
D =
b2 – 4ac =
= (–3)2 –
4 ∙ 2 ∙ 5
= –31.
Задания к уроку 17
Другие уроки:
- Урок 1. Линейные уравнения с одной переменной и целыми свободными членами
- Урок 2. Линейные уравнения с одной переменной и дробными свободными членами
- Урок 3. Применение правил определения неизвестного слагаемого, уменьшаемого и вычитаемого для решения задач
- Урок 4. Применение правил определения неизвестного множителя для решения задач
- Урок 5. Решение уравнений, сводимых к линейным
- Урок 6. Решение уравнений с переменной в знаменателе
- Урок 7. Применение правил опреднления делимого и делителя для решения задач
- Урок 8. Линейные уравнения с двумя переменными
- Урок 9. Решение линейных уравнений с помощью графиков
- Урок 10. Линейные уравнения с параметрами
- Урок 11. Системы уравнений первой степени с двумя неизвестными
- Урок 12. Решение систем уравнений способом подстановки
- Урок 13. Решение систем уравнений способом алгебраического сложения
- Урок 14. Решение линейных систем уравнений с помощью графиков
- Урок 15. Решение задач с помощью систем уравнений первой степени
- Урок 16. Системы линейных уравнений с тремя неизвестными
- Урок 18. Приведённое квадратное уравнение
- Урок 19. Теорема Виета
- Урок 20. Неполные квадратные уравнения
- Урок 21. Решение квадратных уравнений выделением квадрата двучлена
- Урок 22. Графический способ решения квадратных уравнений
- Урок 23. Квадратный трёхчлен
- Урок 24. Квадратные уравнения с параметрами
- Урок 25. Дробные рациональные уравнения
- Урок 26. Решение задач с помощью квадратных уравнений
- Урок 27. Уравнение окружности
- Урок 28. Системы уравнений второй степени с двумя неизвестными
- Урок 29. Решение задач с помощью систем уравнений второй степени
- Урок 30. Пересечение прямой и окружности
- Урок 31. Решение нелинейных систем уравнений с помощью графиков
- Урок 32. Системы уравнений с параметрами
- Урок 33. Уравнения высших стапеней
- Урок 34. Решение уравнений способом замены
- Урок 35. Решение систем уравнений способом замены
- Урок 36. Задачи на нахождение чисел
- Урок 37. Задачи на нахождение цифр
- Урок 38. Решение задач на смешивание с помощью уравнений
- Урок 39. Решение задач на смешивание с помощью систем уравнений
- Урок 40. Иррациональные уравнения
- Урок 41. Уравнения с модулем













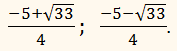











Комментариев нет:
Отправить комментарий