Каждое уравнение с
двумя переменными х и у определяет некоторое множество пар (х; у) значений
переменных, которые являются решениями этого уравнения, т. е. задаёт некоторое
отношение между значениями переменной х и значениями
переменной у. График отношения, заданного уравнением с двумя
переменными, или, короче, график уравнения с двумя переменными, есть, как
известно, множество точек плоскости, координаты которых служат решениями
уравнения. Мы знаем, что графиком уравнения вида ax + by = c,
где a ≠ 0 или b ≠ 0,
служит прямая линия, график уравнения вида
y = ax2 + bx + c (a ≠ 0)
парабола, график уравнения вида
xy = k
гипербола.
На рисунку
изображён график уравнения
х2 + 9у2 = 81.
Кривая такого вида
называется эллипсом.
(x – a)2 + (y – b)2 = r2
является окружность на координатной плоскости хОу с центром в точке О’(a; b) и радиусом r (r > 0).
Составим уравнение окружности
с центром в точке А0(а; b) и радиусом R.
(х – a)2 + (у – b)2.
Таким образом, координаты х, у каждой точки А окружности будут корнями уравнения:
(х – a)2 + (у – b)2 = R2.
Наоборот: любая точка А, координаты которой будут решениями уравнения, принадлежат окружности, так как расстояние от неё до точки А0 равно R. Отсюда вытекает, что это уравнение будет уравнением окружности с центром А0 и радиусом R.
Обратите внимание, что
когда центром окружности будет начало координат, то уравнение окружности имеет
вид:
х2 + у2 = R2.
ПРИМЕР:
Какая геометрическая фигура задано уравнением ?
х2 + у2 + ах + bу + с = 0.
видим, что искомая фигура – окружность с центром
ПРИМЕР:
Построить график уравнения:
х2 + у2 = 16.
Перепишем уравнение в виде
(х – 0)2 + (у – 0)2 = 42.
Графиком этого уравнения является окружность с центром в точке О(0; 0) и радиусом 4.
ПРИМЕР:
Построить график уравнения:
(х – 1)2 + (у – 2)2 = 9.
Перепишем уравнение в виде
(х – 1)2 + (у – 2)2 = 32.
Графиком этого уравнения является окружность с центром в точке (1; 2) и радиусом 3.
ПРИМЕР:
Построить график уравнения:
х2 + у2 + 4х = 0.
Перепишем уравнение в виде
х2 + 4х + 4 + у2 = 4,
(х + 2)2 + у2
= 4,
(х – (–2))2 + (у – 0)2 = 22,
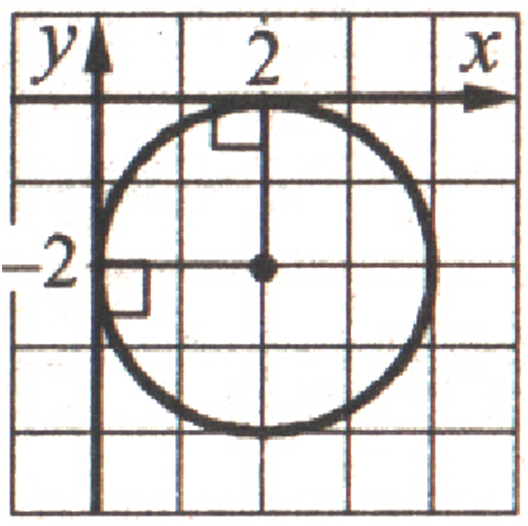
Графиком этого уравнения является окружность с центром в точке (–2; 0) и радиусом 2.
От графиков функций
необходимо отличать графики уравнений.
ПРИМЕР:
На координатной плоскости изображена окружность радиусом r = 5 с центром в начале координат. Уравнение этой окружности:
х2 + у2 = 25.
Можно сказать и так: графиком уравнения
х2 + у2 = 25
будет окружность, изображённая на рисунку.
А можно график уравнения
х2 + у2 = 25
считать графиком некоторой функции ? Нет. Если переменные х и у связаны соотношением
х2 + у2 = 25,
то одному значению х = 3 соответствует два разных значения переменной у: 4 и –4. А соотношение между переменными х и у только тогда считается функцией, когда каждому значению х из области определения соответствует одно значение у. График уравнения только тогда будет графиком некоторой функции, если каждая прямая, параллельная оси у, пересекает его не больше чем в одной точке.
Изображённые на рисунке полуокружности – графики функций
у2 = 25 – х2, или
у2 +
х2 = 25.
ПРИМЕР:
Составьте уравнение окружности,
диаметр которой будет отрезок CD, если
C(–3; 3), D(1; 7).
РЕШЕНИЕ:
О(–1; 5).СО2 = (–1 + 3)2
+ (5 – 3)2 = 8.
Напишите уравнение окружности с
центром в точке
О(2;
–1)
и радиусом равным 3.
РЕШЕНИЕ:
(х – 2)2
+ (у – (–1))2 = 32,
(х – 2)2
+ (у + 1)2 = 9.
ПРИМЕР:
Составьте уравнение окружности,
диаметр которой будет отрезок МК,
если
М(–3;
4), К(5; 10).
РЕШЕНИЕ:
(х – 1)2
+ (у – 7)2 = 25.
ПРИМЕР:
Дано уравнение окружности
(х
+ 7)2 + (у – 4)2 = 16.
Найдите радиус окружности
РЕШЕНИЕ:
(х + 7)2 + (у – 4)2
= 42, R
= 4.
ПРИМЕР:
О(2; –2), R = 2, тому
(х – 2)2 + (у – (–2))2
= 22,
(х – 2)2
+ (у + 2)2 = 4.
Задания к уроку 27
Другие уроки:
- Урок 1. Линейные уравнения с одной переменной и целыми свободными членами
- Урок 2. Линейные уравнения с одной переменной и дробными свободными членами
- Урок 3. Применение правил определения неизвестного слагаемого, уменьшаемого и вычитаемого для решения задач
- Урок 4. Применение правил определения неизвестного множителя для решения задач
- Урок 5. Решение уравнений, сводимых к линейным
- Урок 6. Решение уравнений с переменной в знаменателе
- Урок 7. Применение правил опреднления делимого и делителя для решения задач
- Урок 8. Линейные уравнения с двумя переменными
- Урок 9. Решение линейных уравнений с помощью графиков
- Урок 10. Линейные уравнения с параметрами
- Урок 11. Системы уравнений первой степени с двумя неизвестными
- Урок 12. Решение систем уравнений способом подстановки
- Урок 13. Решение систем уравнений способом алгебраического сложения
- Урок 14. Решение линейных систем уравнений с помощью графиков
- Урок 15. Решение задач с помощью систем уравнений первой степени
- Урок 16. Системы линейных уравнений с тремя неизвестными
- Урок 17. Полное квадратное уравнение общего вида
- Урок 18. Приведённое квадратное уравнение
- Урок 19. Теорема Виета
- Урок 20. Неполные квадратные уравнения
- Урок 21. Решение квадратных уравнений выделением квадрата двучлена
- Урок 22. Графический способ решения квадратных уравнений
- Урок 23. Квадратный трёхчлен
- Урок 24. Квадратные уравнения с параметрами
- Урок 25. Дробные рациональные уравнения
- Урок 26. Решение задач с помощью квадратных уравнений
- Урок 28. Системы уравнений второй степени с двумя неизвестными
- Урок 29. Решение задач с помощью систем уравнений второй степени
- Урок 30. Пересечение прямой и окружности
- Урок 31. Решение нелинейных систем уравнений с помощью графиков
- Урок 32. Системы уравнений с параметрами
- Урок 33. Уравнения высших стапеней
- Урок 34. Решение уравнений способом замены
- Урок 35. Решение систем уравнений способом замены
- Урок 36. Задачи на нахождение чисел
- Урок 37. Задачи на нахождение цифр
- Урок 38. Решение задач на смешивание с помощью уравнений
- Урок 39. Решение задач на смешивание с помощью систем уравнений
- Урок 40. Иррациональные уравнения
- Урок 41. Уравнения с модулем













Комментариев нет:
Отправить комментарий