ax2 + bx + c
положительный, то данный трёхчлен можно разложить на линейные множители.
Рассмотрим задачу
разложения на линейные множители квадратного трехчлена – многочлена второй
степени с одной переменной. Пусть известно, что квадратный трехчлен
ах2 +
bх + с,
где х –
переменная, а, b и с –
числа, причём а ≠ 0, имеет корни х1 и х2.
Покажем, что в этом случае можно подать его в виде произведения:
ах2 +
bх + с = а(х – х1)(х – х2).
Чтобы доказать
тождество, превратим ее правую часть:
а(х – х1)(х – х2) =
а(х2 – х1х – х2х + х1х2) =
а[х2 – (х1 + х2)х + х1х2].
Корни х1 и х2 трёхчлена
ах2 + bх + с
являются корнями уравнения
ах2 + bх + с = 0.
Чтобы разложить квадратный трёхчлен на множители, иногда приходится пользоваться несколькими способами. Сначала применить способ группирования, затем вынесение общего множителя за скобки и затем применение какой-нибудь формулы сокращённого умножения.
ПРИМЕР:
Трёхчлен:
2х2 – 5х – 3
имеет корни, поскольку дискриминант квадратного уравнения
2х2 – 5х – 3 = 0
2х2 – 5х – 3 =
(2х + 1)(х – 3).
Тождество может
распространяться и на квадратный трехчлен, имеющий единый корень. В этом случае
х1 = х2, и тождество примет вид:
ах2 + bх + с =
а(х – х1)(х – х2), тоесть
ах2 +
bх + с = а(х – х1)2.
ПРИКЛАД:
Трёхчлен:
–25х2 + 10х – 1
Имеет единственный корень, равный 1/5 (в этом легко убедиться, решив уравнение
–25х2 + 10х – 1 = 0).
Применяя тождество, получим:
ах2 +
bх + с =
= (kх + m)(pх +q).
ПРИМЕР:
3х2 – 13х – 10.
D =
132 + 4 × 3 ×
10 =
= 289; D > 0.
Разложите на множители:
6х2 – х – 2.
РЕШЕНИЕ:
Применим формулу корней квадратного
уравнения к уравнению
6х2 – х – 2 = 0,
находим
х1 = –1/2, х2 =
2/3.
Значит,
6х2 – х – 2 = 6(х + 1/2)(х – 2/3) =
= 2(х + 1/2)∙3(х – 2/3) = (2х + 1)(3х – 2).
Разложение
на множители двучлена хn – аn.
Известно, что
х2 – а2
= (х – а)(х + а),
х3 – а3
= (х – а)(х2 + ха + а2).
Если перемножить многочлены
(х – а) и (x3
+ х2a + ха2 + а3), то получим
х4 – а4
= (х – а)(x3 +х2a + ха2 + а3).
Обобщением полученных выше формул является формула разложения на множители
двучлена хn – аn
хn – аn =
(х – а)(xn-1
+хn-2a + хn-3а2 + … + xаn-2 + an-1).
Если, в частности, а = 1, то получаем:
хn – 1 = (х – 1)(xn-1 +хn-2 + хn-3 + … + x + 1).
ПРИМЕР:
- Урок 1. Линейные уравнения с одной переменной и целыми свободными членами
- Урок 2. Линейные уравнения с одной переменной и дробными свободными членами
- Урок 3. Применение правил определения неизвестного слагаемого, уменьшаемого и вычитаемого для решения задач
- Урок 4. Применение правил определения неизвестного множителя для решения задач
- Урок 5. Решение уравнений, сводимых к линейным
- Урок 6. Решение уравнений с переменной в знаменателе
- Урок 7. Применение правил опреднления делимого и делителя для решения задач
- Урок 8. Линейные уравнения с двумя переменными
- Урок 9. Решение линейных уравнений с помощью графиков
- Урок 10. Линейные уравнения с параметрами
- Урок 11. Системы уравнений первой степени с двумя неизвестными
- Урок 12. Решение систем уравнений способом подстановки
- Урок 13. Решение систем уравнений способом алгебраического сложения
- Урок 14. Решение линейных систем уравнений с помощью графиков
- Урок 15. Решение задач с помощью систем уравнений первой степени
- Урок 16. Системы линейных уравнений с тремя неизвестными
- Урок 17. Полное квадратное уравнение общего вида
- Урок 18. Приведённое квадратное уравнение
- Урок 19. Теорема Виета
- Урок 20. Неполные квадратные уравнения
- Урок 21. Решение квадратных уравнений выделением квадрата двучлена
- Урок 22. Графический способ решения квадратных уравнений
- Урок 24. Квадратные уравнения с параметрами
- Урок 25. Дробные рациональные уравнения
- Урок 26. Решение задач с помощью квадратных уравнений
- Урок 27. Уравнение окружности
- Урок 28. Системы уравнений второй степени с двумя неизвестными
- Урок 29. Решение задач с помощью систем уравнений второй степени
- Урок 30. Пересечение прямой и окружности
- Урок 31. Решение нелинейных систем уравнений с помощью графиков
- Урок 32. Системы уравнений с параметрами
- Урок 33. Уравнения высших стапеней
- Урок 34. Решение уравнений способом замены
- Урок 35. Решение систем уравнений способом замены
- Урок 36. Задачи на нахождение чисел
- Урок 37. Задачи на нахождение цифр
- Урок 38. Решение задач на смешивание с помощью уравнений
- Урок 39. Решение задач на смешивание с помощью систем уравнений
- Урок 40. Иррациональные уравнения
- Урок 41. Уравнения с модулем
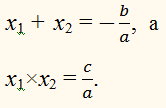








Комментариев нет:
Отправить комментарий