Пусть дано
равенство с переменными х, а:
f(x; a) = 0.
Если ставится
задача для каждого действительного значения
а решить это
уравнение относительно х,
то уравнение f(x; a)
= 0 называют уравнением с переменной х и параметром а.
ОТВЕТ:
ПРИМЕР:
При каких значениях
a уравнение не
имеет корней ?
x2 +
5aх + 5а = 0.
РЕШЕНИЕ:
Данное
уравнение не имеет корней, если его дискриминант отрицательный.
x2 +
5aх + 5а = 0,
D =
(5а)2 – 4∙5a = 25а2 – 20а =
=
5а(5а – 4) <
0, а ∈ (0; 0,8).
ПРИМЕР:
При каких значениях
с уравнение не
имеет корней ?
x2 +
сх + 25 = 0.
РЕШЕНИЕ:
Данное
уравнение не имеет корней, если его дискриминант отрицательный.
x2 +
сх + 25 = 0,
D =
с2 – 4∙25 = с2
– 100 < 0,
(с – 10)(с + 10) <
0, с ∈ (–10; 10).
ПРИМЕР:
При каких значениях
a уравнение не
имеет корней ?
x2 + 2ах + 7а = 0.
РЕШЕНИЕ:
Данное
уравнение не имеет корней, если его дискриминант отрицательный.
x2 +
2ах + 7а = 0,
D =
(2а)2 – 4∙7a = 4а2 – 28а =
= 4а(а
– 7) < 0, а ∈ (0; 7).
ПРИМЕР:
При каких значениях
a уравнение не
имеет корней ?
x2 –
х + а – 5 = 0.
РЕШЕНИЕ:
Данное
уравнение не имеет корней, если его дискриминант отрицательный.
x2 –
х + а – 5 = 0,
D =
(–1)2 – 4(а –
5) = 1 – 4а + 20 =
=
21 – 4а < 0, 4а > 21, а > 5,25,
а ∈ (5,25; +∞).
ПРИМЕР:
При каких значениях b уравнение имеет два разных корня ?
x2 + bx + 49 = 0.
РЕШЕНИЕ:
Данное
уравнение будет иметь два разных корня, когда его дискриминант будет
положительным.
x2 +
bx + 49 = 0,
D =
b2 – 4∙49 = b2
– 196 > 0,
(b – 14)(b + 14) > 0,
b ∈ (–∞; –14)
∪ (14; +∞).
ПРИМЕР:
При каких значениях
b уравнение не имеет корней ?
5x2 + bх +
20 = 0.
РЕШЕНИЕ:
Данное
уравнение не имеет корней, если его дискриминант отрицательный.
5x2 + bх +
20 = 0,
D =
b2 – 4∙5∙20 = b2 – 400 < 0,
(b – 20)(b + 20) > 0,
b ∈ (–20; 20).
ПРИМЕР:
Число –3 является корнем
уравнения
x2 +
bх –
12 = 0.
Найдите другой корень уравнения.
РЕШЕНИЕ:
Из теоремы Виета
х1 ∙ х2 = –12,
–3х2 = –12, х2 = 4.
ПРИМЕР:
Число –3 является корнем
уравнения
3x2 + 2х + с = 0.
Найдите другой корень уравнения.
РЕШЕНИЕ:
Поскольку число –3 является корнем, то оно удовлетворяет уравнение:
3 ∙ (–3)2 + 2 ∙ (–3) + с = 0,
27 – 6 + с = 0,
с = –21.
Уравнение:
3x2 + 2х – 21 = 0,
(3х – 7)(х + 3) = 0,
х1 = –3, х2
= 21/3.
ПРИМЕР:
Решите уравнение:
(а –1)x2
+ 2(2а + 1)х +
4а + 3 = 0.
РЕШЕНИЕ:
Выделим особо значение
параметра а = 1. Дело в том, что при
а = 1 данное уравнение
не является квадратным, а при а ≠ 1 оно квадратное.
Решать уравнение в каждом из
этих случаев надо по-своему. При а = 1 уравнение
принимает вид 6х + 7 = 0, откуда находим
х
= –7/6.
В случае, если а ≠ 1 для квадратного
уравнения выделим те значения параметра, при которых дискриминант уравнения
обращается в нуль.
Имеем:
D/4 = 5а + 4.
Значит,
а
= –4/5.
значение параметра на которое
нам надо обратить внимание.
Если
а < –4/5, D < 0
и, следовательно, уравнение не
имеет действительных корней.
Если
а
= –4/5, то D
= 0.
если а < –4/5 то действительных корней нет,
если а
= 1, то х = –7/6,
если а
= –4/5,
то х
= –1/3,
При каком значении
параметра а уравнение
х2 + 2(а + 1)х + 9а – 5 = 0
имеет два различных
отрицательных корня.
РЕШЕНИЕ:
Так как уравнение должно иметь
два различных действительных корня х1 и х2, его дискриминант
должен быть положительным. Имеем:
D = 4(а + 1)2
– 4(9а – 5) =
=
4а2 – 28а + 24 = 4(а – 1)(а – 6).
Значит должно выполняться
неравенство:
4(а – 1)(а – 6) ˃ 0.
По теореме Виета для заданного
уравнения имеем:
х1 + х2
= –2(а + 1),
х1 х2 = 9а – 5.
Так как, по условию,
х1 < 0 и х2
< 0, то
–2(а + 1) < 0 и 9а
– 5 > 0.
Из второго неравенства находим а > –1.
Из третьего неравенства находим а > 5/9.
- Урок 1. Линейные уравнения с одной переменной и целыми свободными членами
- Урок 2. Линейные уравнения с одной переменной и дробными свободными членами
- Урок 3. Применение правил определения неизвестного слагаемого, уменьшаемого и вычитаемого для решения задач
- Урок 4. Применение правил определения неизвестного множителя для решения задач
- Урок 5. Решение уравнений, сводимых к линейным
- Урок 6. Решение уравнений с переменной в знаменателе
- Урок 7. Применение правил опреднления делимого и делителя для решения задач
- Урок 8. Линейные уравнения с двумя переменными
- Урок 9. Решение линейных уравнений с помощью графиков
- Урок 10. Линейные уравнения с параметрами
- Урок 11. Системы уравнений первой степени с двумя неизвестными
- Урок 12. Решение систем уравнений способом подстановки
- Урок 13. Решение систем уравнений способом алгебраического сложения
- Урок 14. Решение линейных систем уравнений с помощью графиков
- Урок 15. Решение задач с помощью систем уравнений первой степени
- Урок 16. Системы линейных уравнений с тремя неизвестными
- Урок 17. Полное квадратное уравнение общего вида
- Урок 18. Приведённое квадратное уравнение
- Урок 19. Теорема Виета
- Урок 20. Неполные квадратные уравнения
- Урок 21. Решение квадратных уравнений выделением квадрата двучлена
- Урок 22. Графический способ решения квадратных уравнений
- Урок 23. Квадратный трёхчлен
- Урок 25. Дробные рациональные уравнения
- Урок 26. Решение задач с помощью квадратных уравнений
- Урок 27. Уравнение окружности
- Урок 28. Системы уравнений второй степени с двумя неизвестными
- Урок 29. Решение задач с помощью систем уравнений второй степени
- Урок 30. Пересечение прямой и окружности
- Урок 31. Решение нелинейных систем уравнений с помощью графиков
- Урок 32. Системы уравнений с параметрами
- Урок 33. Уравнения высших стапеней
- Урок 34. Решение уравнений способом замены
- Урок 35. Решение систем уравнений способом замены
- Урок 36. Задачи на нахождение чисел
- Урок 37. Задачи на нахождение цифр
- Урок 38. Решение задач на смешивание с помощью уравнений
- Урок 39. Решение задач на смешивание с помощью систем уравнений
- Урок 40. Иррациональные уравнения
- Урок 41. Уравнения с модулем








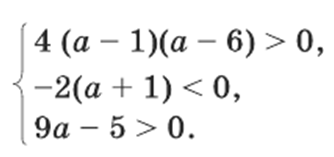

Комментариев нет:
Отправить комментарий