Уроки математики и физики (RU + UA)

▼

вторник, 27 ноября 2018 г.

Урок 22. Квадрат

ВИДЕОУРОК

Квадрат – прямоугольник, у которого все стороны равны.

ABCD – квадрат,
AB = BC = CD = AD,

∠ A = ∠ B = ∠ C = ∠ D = 90°.

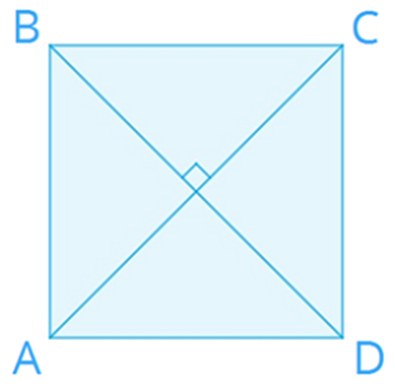
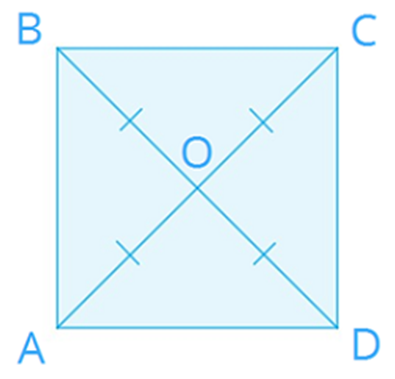
Свойства квадрата.

– все стороны квадрата равны;
– все углы квадрата прямые;
– диагонали квадрата равны;
– диагонали квадрата взаимно перпендикулярны;
– диагонали квадрата точкой пересечения делятся пополам;
– диагонали квадрата делят углы квадрата пополам;
– диагонали квадрата делят его на четыре равных прямоугольных равнобедренных треугольника.
Формулы для нахождения диагонали квадрата.
ЗАДАЧА:

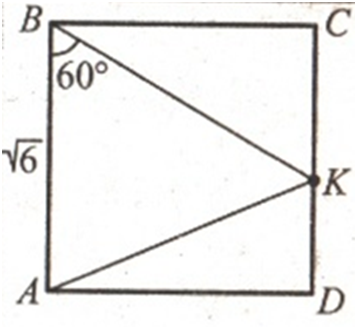
На стороне  CD  квадрата  ABCD  обозначена точка  К  так, что

∠ AВК = 60°.

Найдите отрезок  AК, если 

ВС = √͞͞͞͞͞6 см.

РЕШЕНИЕ:

Начертим чертёж:
ABCD – квадрат,

∠ AВК = 60°,

ВС = √͞͞͞͞͞6 см.

По условию 

∠ AВК = 60°, тогда 

∠ КВС = 90° – 60° = 30°.

Рассмотрим  ∆ ВСК (∠ С = 90°).

Так как угол  ∠ КВС = 30°, то против угла в  30°  лежит катет, равный половине гипотенузы, то есть  ВК = 2СК. Обозначим 

СК = х, тогда  ВК = 2х.

По теореме Пифагора запишем:

ВК2 = ВС2 + СК2,

(2СК)2 = ВС2 + СК2,

3СК2 = (√͞͞͞͞͞6)2,

СК2 = 2, СК = √͞͞͞͞͞2 (см).

КD = СD – СК = (√͞͞͞͞͞6 – √͞͞͞͞͞2) (см).

Рассмотрим  ∆ АКD (∠ D = 90°).

АК2 = АD2 + КD2 =

= (√͞͞͞͞͞6 )2 + (√͞͞͞͞͞6 – √͞͞͞͞͞2)2 =

= 6 + 6 – 2√͞͞͞͞͞12 + 2 =

= 14 – 4√͞͞͞͞͞3.

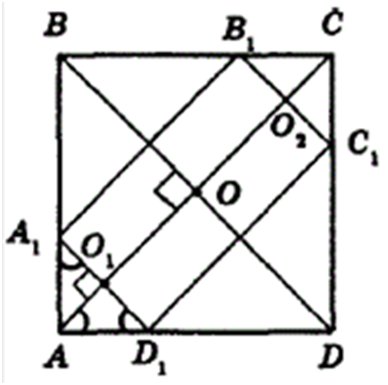
ЗАДАЧА:

В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Найдите стороны прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна  12 м.

РЕШЕНИЕ:

Начертим чертёж.
∠ ВОА = 90° (диагонали квадрата пересекаются под прямым углом).

∠ ВОА = ∠ А1О1А = 90°  (как соответственные углы для параллельных прямых  ВD  и  А1D, и секущей  АС).

АС – биссектриса, поэтому

∠ А1АО1 = ∠ О1АD1 =

= 1/2 ∠ А = 45°.

Значит,

∠ АА1О1 = ∠ АD1О1 = 45°.

∆ А1АD1 – равнобедренный, так как  АО1  является высотой, биссектрисой, а значит и медианой.

Значит 

А1О1 = О1D1, 

∆ АО1D1 – равнобедренный, поэтому 

АО1 = О1D1.

Так что 

А1О1 = АО1 = О1D1.

Пусть отрезок  А1О1 = х м, тогда 

А1D1 = 2х м  и 

А1В1 = 2А1D1 = 4 м.

Далее,

АС = АО1 + О1О2 + О2С =

= АО1 + А1В1 + О2С.

х + 4х + х = 12,

6х = 12 м, х = 2 м.

Тогда 

А1D1 = 2х = 2 ∙ 2 = 4 (м).

А1В1 = 4х = 8 (м).

А1D1 = В1С1 = 4 (м),

А1В1 = D1С1 = 8 (м).

ОТВЕТ:  4 м, 8 м

ЗАДАЧА:

В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две других – на катетах. Найдите сторону квадрата, если гипотенуза равна  3 м.

РЕШЕНИЕ:

Начертим чертёж.
∆ АВС – прямоугольный, равнобедренный, тогда, 

∠ АВС = ∠ АСВ =

= 1/2 (180° – 90°) = 45°.

∆ DКС – равнобедренный, так как 

∠ DКС = 90°, ∠ АСК = 45°,

тогда и  ∠ КDС = 45°.

Значит  DК = КС.

Аналогично и  ∆ ВLЕ – равнобедренный и

ВЕ = LЕ,

LЕ = КD = ЕК – стороны квадрата.

Пусть  ВЕ = х м. Тогда 

ЕК = КС = х м,

ВС = ВЕ + ЕК + КС =

= 3х = 3 м,

х = 1 м.

Откуда  ЕК = 1 м.

ОТВЕТ:  1 м

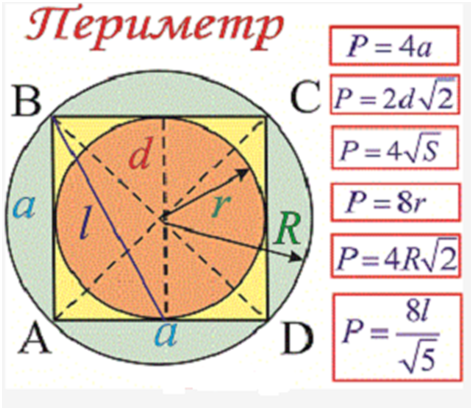
Периметр квадрата.

На практике очень часто приходится решать задачи по определению периметра квадрата.

Квадрат  – это фигура, лежащая в одной плоскости. Если мы измерим и сложим все стороны квадрата, то получим число, которое называется периметром данного квадрата. Если в квадрате обозначим сторону  а, то периметр квадрата  Р  будет равен:
Найти периметр квадрата – это значит вычислить сумму его сторон. Если периметр – это сумма длин всех сторон фигуры, то полупериметр – сумма двух сторон квадрата.
Формулы для нахождения периметра квадрата.
ЗАДАЧА:

Сумма диагоналей квадрата равна  2√͞͞͞͞͞2. Найдите его периметр.

РЕШЕНИЕ:

Если сумма диагоналей равна  2√͞͞͞͞͞2, а диагонали квадрата равны, то одна диагональ равна  √͞͞͞͞͞2. Так как диагональ квадрата в  √͞͞͞͞͞2  раз больше стороны, то сторона равна  1. Значит, периметр квадрата будет равен  4.

ЗАДАЧА:

В равнобедренный прямоугольный треугольник вписан квадрат так, что они имеют общий прямой угол. Найдите периметр квадрата, если катет треугольника равен  4 см.

РЕШЕНИЕ:

Рассмотрим  ∆ ВРС  и  ∆ МСК.
Они равнобедренные, так как прямоугольные с острым углом  45°  (углы  Р  и  К – углы равнобедренного треугольника по условию) и имеют равные стороны 

РВ = ВС = СМ = МК.

Также  ∆ ВРС = ∆ МСК  по двум катетам или за катетом и острым углом. Поэтому, сторона квадрата равна половине катета заданного равнобедренного прямоугольного треугольника. Периметр квадрата  АВСМ   

2 × 4 = 8 (см).

ОТВЕТ:  8 см.

ЗАДАЧА:

Через вершины квадрата с периметром  8√͞͞͞͞͞2 см  проведены прямые  параллельные его диагоналям. Найдите периметр полученного четырёхугольника.

РЕШЕНИЕ:

Начертим чертёж.
Дано: квадрат  KLMN, у которого сторона  KL  равна 

8√͞͞͞͞͞2  : 4 = 2√͞͞͞͞͞2 (см).

Рассмотрим треугольник  KBL. Он равнобедренный и прямоугольный, в котором  

KL = 2√͞͞͞͞͞2 (см) – гипотенуза.

Обозначим

КВ = ВL = х,

тогда по теореме Пифагора, получим:

х2 + х2 = (2√͞͞͞͞͞2)2,

Найдём  х.

2х2 = 8, х2 = 4,

х = 2.

Это половина стороны четырёхугольника, который является квадратом, значит, его периметр равен: 

2 ∙ 2 ∙ 4 = 16 (см).

Задания к уроку 22
Другие уроки:
на

Комментариев нет:

Отправить комментарий