Треугольником
называют геометрическую фигуру, которая состоит из трёх точек, не лежащих на
одной прямой, трёх отрезков, которые соединяют эти точки, и ограниченной этими
отрезками плоскости. Точки А, В и С называются вершинами, а отрезки
АВ, ВС, АС – сторонами треугольника.
Треугольник
называют и обозначают по его вершинам. Треугольник, изображённый на рисунке,
обозначают так ∆ АВС
(читают: треугольник АВС), или ∆ ВСА,
или ∆ АСВ.
Углы АВС, ВАС, АСВ – углы треугольника
АВС. Углы
можно обозначать и одной буквой: ∠ В, ∠ А, ∠ С. Стороны треугольника
АВС можно обозначать маленькими буквами a, b и c. При
этом придерживаются такого порядка: против угла
А находится
сторона а или ВС; против угла В находится
сторона b или АС; против угла С находится сторона с или АВ. Угол В называют углом,
противоположным стороне АС, а углы А и С –
прилегающими к этой стороне.
Построение треугольников.
ЗАДАЧА:
Постройте треугольник
АВС, в
котором
АВ = 5 см,
ВС = 4 см,
∠ В
= 40°.
РЕШЕНИЕ:
Начертим луч
ВМ. С помощью транспортира построим угол МВN, градусная мера которого 40°.От вершины В на стороне ВM этого угла отложим
отрезок ВА длиной
5 см,
а на стороне ВN – отрезок ВС длиной
4 см.
Соединив точки А и С отрезком, получим треугольник АВС.
ЗАДАЧА:
Постройте треугольник
АВС, в
котором
АВ = 6 см,
∠ А
= 60°,
∠ В
= 20°.
РЕШЕНИЕ:
Начертим отрезок
АВ длиной 6 см.С помощью транспортира построим с одной стороны от прямой АВ угол ВАN, который равен 60°, и угол АВК, который
равен 20°.
Точка пересечения лучей АN и ВК и будет третьей вершиною С треугольника
АВС. ЗАДАЧА:
Постройте треугольник
АВС, в
котором
АВ = 3,5 см,
АС = 3 см,
ВС = 4 см.
РЕШЕНИЕ:
Начертим отрезок
АВ длиной 3,5 см. Вершина С будет удалена от точки А на 4 см, поэтому она должна лежать на окружности с
центром А и радиусом 4 см.Вершина С должна быть удалена
от точки В на 3 см, поэтому она должна лежать на окружности с
центром В и радиусом
3
см. Построим эти две окружности. Одну из точек пересечения обозначим С и соединим её с точками А и В.
Если соединить три
пластины так, как показано на рисунку,то, ни растянуть, ни сжать и не согнуть пластины
нельзя, то есть нельзя изменить форму треугольника. Говорят, что треугольник – жёсткая
фигура. Этим свойством треугольника пользуются на практике.Длины отрезков, с помощью которых строят треугольник,
не могут задаваться произвольно. Сумма длин коротких пластин на рисункуменьше чем длина
большой пластины. Поэтому, если крутить короткие пластины вокруг точек А и В, их концы С и D никогда не соединятся и треугольник не получится.Треугольник можно
построить по трём сторонам, если длина большой стороны меньше чем сумма длин двух
других сторон
ПРИМЕР:
Существует ли треугольник АВС со сторонами:
АВ = 5 см,
АС = 18 см,
ВС = 7 см.
РЕШЕНИЕ:
АС наибольшая сторона, равная 18 см. Сумма двух других сторон равна 13 см, она меньше длины большей стороны, значит треугольник
построить нельзя.
ПРИМЕР:
Существует ли треугольник АВС со сторонами:
АВ = 7 см,
АС = 8 см,
ВС = 12 см.
РЕШЕНИЕ:
ВС наибольшая сторона, равная 12 см. Сумма двух других
сторон равна 15 см, она больше длины большей стороны, значит треугольник построить
можно
Средняя линия –
прямая, соединяющая середины двух сторон треугольника, параллельна третьей
стороне и равна её половине.
Например: в треугольнике АВС отрезок
МN –
средняя линияТреугольник имеет
три средних линии. При
проведении всех трёх средних линий образуются
4 равных треугольника.
Например: в
треугольнике АВС отрезок МN –
средняя линияСвойства сторон и углов треугольника.
Любая сторона треугольника
меньше суммы двух других сторон и больше чем их разность.
c –
b < a < c + b,
b < c.
Чтобы проверить,
можно или нет из трёх отрезков а, b и с получить
треугольник, надо проверить, будет или нет самый длинный из этих отрезков
меньше, чем сумма двух других. ЗАДАЧА:
В треугольнике АВС известно, что
АВ = 5 см, ВС
= 10 см.
Какая из приведённых величин
может быть равна длине стороны АВ ?
4 см,
5 см,
8 см,
17 см.
РЕШЕНИЕ:
АВ – ВС < АС < АВ + ВС,
10 – 5 < АС < 10 + 5,
5 < АС < 15.
Поэтому, АС = 8 см.
Сумма
углов треугольника равна 180°.
Против большей
стороны треугольника лежит и больший угол: если b > а, то β > α; и наоборот, если β > α, то b > а; а также,
если а = b, то α = β.
ЗАДАЧА:
В треугольнику АВС
∠ А
= 30°, ∠ В = 45°.
Какая сторона треугольника будет наибольшей ?
РЕШЕНИЕ:
Найдём угол С.
∠ С
= 180° – (30° + 45°) = 105°.
∠ С
– наибольший, поэтому наибольшей стороною будет АВ.
Внешним
углом треугольника (∠ КВС) называют угол, полученный стороною
треугольника и продолжением его другой стороны.
При каждой вершине
есть два внешних угла. Внешний угол треугольника равен сумме двух внутренних углов
треугольника, не смежных с ним.
∠ КВС =
∠ АСВ + ∠ САВ.
Внешний угол
треугольника больше каждого внутреннего угла, не смежного с ним. Если каждая из
двух фигур (треугольников) равна третьей, то первая и вторая фигура
(треугольник) тоже равны.
Сумма внешних
углов треугольника, взятых по одному при каждой вершине,
равна 360°.
∠ 1 + ∠ 2 + ∠ 3 = 360°.
Треугольник, у
которого все стороны разные, называется разносторонним.
Треугольник
разбивает плоскость на две области: внутреннюю и внешнюю. Фигура, которая
состоит из треугольника и его внутренней области, тоже называется
треугольником. Углами треугольника АВС называют углы ВАС, АВС и АСВ.
Их обозначают так: ∠ А, ∠ В, ∠ С. Каждый треугольник имеет три угла.
Если треугольник
имеет тупой угол, его называют тупоугольным
треугольником. Треугольник, у которого все углы острые, называется остроугольным. Треугольник не может иметь
двух прямых или двух тупых углов. У каждого треугольника как правило два угла –
острые. Если один из углов – тупой, то два других угла – острые. В каждом
треугольнике против большей стороны лежит больший угол, а против большего угла
– большая сторона.
Два треугольника
называются равными, если при наложении друг на друга они совмещаются.
При обозначении
вершин равных треугольников имеет значение порядок записи букв: буквы, которые
соответствуют равным углам, необходимо записывать в обоих треугольниках на
одинаковых местах.
В равных
треугольниках против равных сторон лежат равные углы, а против равных углов –
равные стороны.
Общие признаки равенства треугольников.
– если две стороны и угол между ними одного треугольника
равны соответственно двум сторонам и углу между ними другого треугольника, то
такие треугольники равны;
– если сторона и
прилегающие к ней углы одного
треугольника равны соответственно стороне и прилегающим к ней углам другого треугольника, то такие треугольники
равны;
– если три стороны одного треугольника равны
соответственно трём сторонам другого треугольника, то такие треугольники равны.
ЗАДАЧА:
Измерить расстояние между двумя
точками на местности, между которыми есть препятствие (нельзя пройти напрямую
и измерить).
РЕШЕНИЕ:
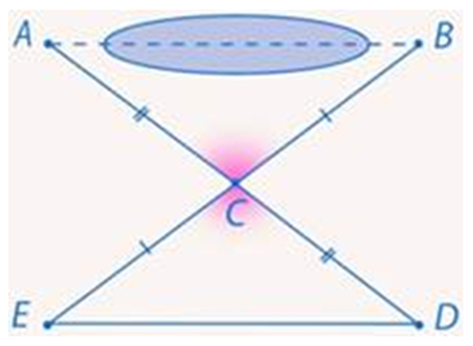
Предположим, что между точками А и В
находится озеро. Надо измерим расстояние между ними.Выберем точку С,
от которой можно пройти по прямой до обеих точек А и В. Получился треугольник
АСВ.
Если построить ему равный
треугольник, где есть доступ ко всем трём сторонам, то задача будет решена.
Продолжим сторону АС и отложим на ней отрезок СD = АС. Аналогично построим
отрезок СЕ = ВС.Полученный треугольник DСЕ
равен
треугольнику АСВ, так как углы ∠ ЕСD, ∠ АСВ равны,
как вертикальные, а стороны СD = АС, СЕ = ВС по построению.
Значит, отрезки АВ и ЕD равны с той разницей,
что отрезок ЕD можно измерить.
Соотношения между элементами произвольного
треугольника.
Квадрат стороны,
лежащей против острого угла, равен сумме квадратов двух других сторон без удвоенного
произведения одной из этих сторон и проекции на неё другой стороны.
c2 = a2 + b2 – 2aba = a2 + b2 – 2bab.
Квадрат стороны, лежащей
против тупого угла, равен сумме квадратов двух других сторон, сложенной с
удвоенным произведением одной из этих сторон и проекции на её продолжение другой
стороны.
c2 = a2 + b2 + 2aba = a2 + b2 + 2bab.
Задания к уроку 6

















Комментариев нет:
Отправить комментарий