Урок 9. Прямоугольный треугольник (2)

ВИДЕОУРОК

Высота прямоугольного треугольника.

Высотой прямоугольного треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

В прямоугольном треугольнике высоты, опущенные из вершин острых углов, совпадают с катетами треугольника, а высота, опущенная из вершины прямого угла на гипотенузу, делит треугольник на два треугольника, подобных исходному и подобных друг другу.

Длина высоты треугольника  АВС

проведённой к гипотенузе  ВС находится по формуле:

АК² = ВК ∙ КС.

где  ВК  и  КС – проекции катетов на гипотенузу.

В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов:

В прямоугольном треугольнике высота, проведённая из прямого угла, равна произведению катетов, делённому на гипотенузу.

Каждый катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключённым между катетом и высотой, проведённой из вершины прямого угла.

Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.

                                    
Высоты  h_a  и  h_b  совпадают с катетами  b  и  a.

Отрезок  XY  есть среднее пропорциональное (или среднее геометрическое) между отрезками  АВ  и  СD, если

ЗАДАЧА:

В треугольнике  АВС: 

∠ С = 90°,

∠ А = 30°, 

АВ = 2√͞͞͞͞͞3.

Найдите высоту  СН.

РЕШЕНИЕ:

Начертим чертёж.

Так как катет, лежащий против угла  30°, равен половине гипотенузы, то

ВС = 0,5АВ = √͞͞͞͞͞3.

Найдём катет  АС  в треугольнике  АВС, пользуясь теоремой Пифагора:

АВ² = АС² + ВС²,

АС² = АВ² – ВС² =

= (2√͞͞͞͞͞3)² – (√͞͞͞͞͞3)² =

 =12 – 3 = 9, АС = 3.

В треугольнике  АНС: АС – гипотенуза, НС – катет, лежащий против угла  30°, значит

НС = 3 : 2 = 1,5.

ЗАДАЧА:

В треугольнике  АВС: 

∠ С = 90°,

∠ А = 30°, 

СН – высота.

Найдите  АН, если  АВ = 2.

РЕШЕНИЕ:

Начертим чертёж.

Так как катет, лежащий против угла  30°, равен половине гипотенузы, то

ВС = 0,5АВ = 1.

Тогда по теореме Пифагора из треугольника  АВС:

Из прямоугольного треугольника  АНС:

НС = 0,5АС = √͞͞͞͞͞3 : 2.

Тогда по теореме Пифагора:

ЗАДАЧА:

В треугольнике  АВС: 

∠ С = 90°,

∠ А = 30°, 

СН – высота.

Найдите  ВН, если  АВ = 4.

РЕШЕНИЕ:

Начертим чертёж.

Так как катет, лежащий против угла  30°, равен половине гипотенузы, то

ВС = 0,5АВ = 2.

Угол  ВСН  равен  30° (90° – 60°),

значит  ВН = 0,5ВС = 1.

ЗАДАЧА:

В прямоугольном треугольнике  АВС  высота  АК  делит гипотенузу на отрезки

ВК = 3 см,

КС = 2 см.

Найдите  катеты треугольника.

РЕШЕНИЕ:

Найдём квадрат длины высоты  АК  пользуясь формулой

АК² = ВК ∙ КС = 3 ∙ 2 = 6.

Рассмотрим прямоугольные треугольники  АКС  и  ВКС, и найдём в них стороны  АС  и  АВ.

Медиана прямоугольного треугольника.

Медиана – это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Для прямоугольного треугольника это будут медианы, проведённые с острого угла к серединам катетов или с прямого к центру гипотенузы.

Свойства медианы в прямоугольном треугольнике.

– медианы в прямоугольном треугольнике пересекаются в одной точке, а точка пересечения делит их в соотношении два к одному считая от вершины, из которой проведена медиана;

– медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузу;

– медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу окружности, описанной вокруг данного прямоугольного треугольника;

– сумма квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам медианы, опущенной на гипотенузу;

– сумма квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти четвёртых квадрата гипотенузы;

– медиана, опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов катетов;

– медиана, опущенная на гипотенузу, равна частному от деления длины катета на два синуса противолежащего катету острого угла;

– медиана, опущенная на гипотенузу, равна частному от деления длины катета на два косинуса прилежащего катету острого угла;

– сумма квадратов сторон прямоугольного треугольникаравна восьми квадратам медианы, опущенной на его гипотенузу;

– медиана, проведённая к катету  а, равна половине корня квадратного из суммы учетверённого квадрата катета  b  и квадрата катета  а;

– медиана, проведённая к катету  b, равна половине корня квадратного из суммы учетверённого квадрата катета  а  и квадрата катета  b;

Обозначения в формулах.

a, b – катеты прямоугольного треугольника;

с – гипотенуза прямоугольного треугольника.

Если обозначить треугольник, как  АВС, то

ВС = а, АС = b, АВ = с

(то есть стороны  а, b, с – являются противолежащими соответствующим углам).

т_а – медиана, проведённая к катету  а;

т_b – медиана, проведённая к катету  b;

т_с – медиана, проведённая к гипотенузе  с;

α (альфа) – угол  САВ, противолежащий стороне  а.

ЗАДАЧА:

Две стороны треугольника равны  6 см  и  8 см. Медианы, проведённые к этим сторонам, пересекаются под прямым углом. Найдите третью сторону треугольника.

РЕШЕНИЕ:

Начертим чертёж.

Обозначим  

АN = х см. ВМ = у см.

Тогда 

АО = ²/₃ х, NО = ¹/₃ у,

ВО = ²/₃ х, МО = ¹/₃ у.

АМ² = ОМ² + ОА²,

ВN² = ОВ² + ОN²,

5х² + 5у² = 225,

х² + у² = 45.

АВ² = ВО² + ОА² =

= ⁴/₉ (х² + у²) = 20, то

АВ = √͞͞͞͞͞20 = 2√͞͞͞͞͞5 см.

ЗАДАЧА:

В треугольнике  АВС:

АВ = √͞͞͞͞͞41, ВС = 13, 

ВН – высота, опущенная на сторону  АС, ВН = 5. 

Найдите длину медианы АМ.

РЕШЕНИЕ:

Начертим чертёж.

В прямоугольном треугольнике  ВНС  по теореме Пифагора 

В прямоугольном треугольнике  АВН  по теореме Пифагора 

Опустим из точки  М  перпендикуляр  МD  на сторону АС, МD – средняя линия треугольника  ВНС, следовательно

МD = ¹/₂ ВН = ⁵/₂,

НD = DС = ¹/₂ НС = 6.

Тогда в прямоугольном треугольнике  АМD

∠ АDМ = 90°,

АD = АН + НD =

= 4 + 6 = 10,

МD = ⁵/₂.

По теореме Пифагора

ЗАДАЧА:

В прямоугольном треугольнике медианы, проведённые к катетам равны  √͞͞͞͞͞52  и √͞͞͞͞͞73. Найдите длину гипотенузы.

РЕШЕНИЕ:

Начертим чертёж.

Проведём медианы  АК  и  ВМ. Пусть 

АК = √͞͞͞͞͞52,

ВМ = √͞͞͞͞͞73,

х – половина длины стороны  АС,

у – половина длины стороны  ВС. Тогда из прямоугольных треугольников  АСК  и  ВСМ  имеем:

АК² = АС² + СК²,

ВМ² = МС² + ВС²

тогда  составим систему уравнений:

отсюда

5(х² + у²) = 125,

х² + у² = 25,

АК² = 4(х² + у²).

АВ = 10.

ЗАДАЧА:

Медианы  СМ  и  ВN  прямоугольного треугольника  АВС (∠ С = 90°), перпендикулярны. Найдите катеты, если гипотенуза равна  с.

РЕШЕНИЕ:

Начертим чертёж.

МА = МС = МВ = ^с/₂.

Пусть  NО = х,

Тогда 

ВО = ²/₃ х, МО = ^с/₆.

МВ² = МО² + ВО²,

Биссектриса прямоугольного треугольника.

Биссектрисою прямоугольного треугольника называют отрезок биссектрисы угла треугольника, который соединяет его вершину с точкой на противоположной стороне треугольника.

Биссектриса прямоугольного треугольника делит противоположную сторону на отрезки, соответственно пропорциональные двум другим сторонам.

Связь угла  (α)  между высотой и биссектрисой, проведёнными из прямого угла, определяется через острые углы этого треугольника.

ЗАДАЧА:

Биссектриса прямого угла прямоугольного треугольника образует с гипотенузой углы, один из которых равен  70°. Найдите острые углы этого треугольника.

РЕШЕНИЕ:

Начертим чертёж.

∠ DBC = ∠ DBA = 45°,

∠ DCB = 180° – 70° – 45° = 65°,

∠ ADB = 180° – 70° = 110°,

∠ CAB = 180° – 110° – 45° = 25°.

ЗАДАЧА:

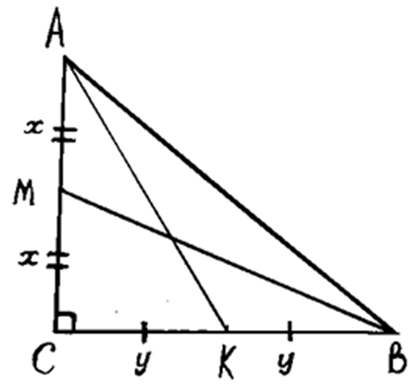
Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной  15 см  и  20 см. Найдите длины отрезков гипотенузы, на которые её делит высота треугольника.

РЕШЕНИЕ:

Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам.

Следовательно,

СВ : АС = 15 : 20.

Пусть коэффициент этого отношения будет  х. Тогда

АС = 20х, ВС = 15х,

АВ = 20 + 15 = 35.

По теореме Пифагора:

АС² + ВС² = АВ^2,

400х² + 225х² = 1225.

х = √͞͞͞͞͞1,96 = 1,4,

АС = 20 ∙ 1,4 = 28,

ВС = 15 ∙ 1,4 = 21.

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключённым между катетом и высотой.

ВС² = АВ ∙ ВН,

441 = 35 ∙ ВН,

ВН = 12,6,

АН = 35 – 12,6 = 22,4.

ЗАДАЧА:

Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен  14°. Найдите меньший угол этого треугольника.

РЕШЕНИЕ:

Начертим чертёж.

Так как связь угла  (α)  между высотой и биссектрисой, проведёнными из прямого угла, определяется через острые углы этого треугольника следующим образом:

∠ ВАС = 45° – α,

∠ ВСА = 45° + α,

∠ α = ∠ МВD = 14°,

то меньший угол треугольника  ВАС  будет равен:

∠ ВАС = 45° – 14° = 31°.

Задания к уроку 9

• Задание 1
• Задание 2
• Задание 3

Другие уроки:

• Урок 1. Точка и прямая
• Урок 2. Угол
• Урок 3. Параллельные и перпендикулярные прямые
• Урок 4. Окружность
• Урок 5. Угол и окружность
• Урок 6. Треугольник (1)
• Урок 7. Треугольник (2)
• Урок 8. Прямоугольный треугольник (1)
• Урок 10. Равнобедренный треугольник (1)
• Урок 11. Равнобедренный треугольник (2)
• Урок 12. Периметр треугольника
• Урок 13. Периметр равнобедренного (равностороннего) треугольника
• Урок 14. Треугольник и окружность
• Урок 15. Прямоугольный треугольник и окружность
• Урок 16. Равнобедренный треугольник и окружность
• Урок 17. Четырёхугольники
• Урок 18. Параллелограмм
• Урок 19. Периметр параллелограмма
• Урок 20. Прямоугольник
• Урок 21. Периметр прямоугольника
• Урок 22. Квадрат
• Урок 23. Ромб
• Урок 24. Периметр ромба
• Урок 25. Трапеция
• Урок 26. Равнобедренная трапеция
• Урок 27. Периметр трапеции
• Урок 28. Четырёхугольник и окружность (1)
• Урок 29. Четырёхугольник и окружность (2)
• Урок 30. Многоугольник
• Урок 31. Правильный многоугольник
• Урок 32. Осевая и центральная симметрии