С помощью уравнений
решаются многочисленные задачи, к которым приводят самые разнообразные вопросы
физики, механики, экономики и так далее.
Общий порядок решения задач с
помощью уравнений.
– вводят переменные, то есть буквами х,
у, z
обозначают
неизвестные величины, которые либо требуется найти в задаче, либо они
необходимы для отыскания искомых величин;
– с помощью введенных переменных и данных в задаче
чисел и их соотношений составляют систему уравнений (или одно уравнение);
– решают составленную систему уравнений (или уравнение) и из полученных решений отбирают те, которые подходят по смыслу задачи;
ЗАДАЧА:
Для перевозки 60 т груза из одного
места в другое затребовали некоторое количество машин. Ввиду неисправности
дороги на каждую машину пришлось грузить на
0,5 т меньше, чем предполагалось, поэтому
дополнительно потребовались 4 машины. Какое количество машин было затребовано
первоначально ?
РЕШЕНИЕ:
что на 0,5 т меньше, чем предполагалось. В результате мы приходим к уравнениюЭто уравнение имеет два корня: х = –24, х = 20. Ясно, что по смыслу задачи значение х = –24 не подходит. Таким образом, первоначально было затребовано 20 машин.
ОТВЕТ: 20 машин
ЗАДАЧА:
Моторная лодка, движущаяся со скоростью 20
кмчас, прошла расстояние между двумя пунктами по реке
туда и обратно без остановок за 6 час 15
мин. Расстояние между пунктами равно 60 км. Найдите скорость течения реки.
РЕШЕНИЕ:
ЗАДАЧА:
Двое рабочих, работая вместе, выполнили некоторую работу
за 6 час.
Первый из них, работая отдельно, может выполнить всю работу на 5
час скорее, чем второй рабочий, если
последний будет работать отдельно. За сколько часов каждый из них, работая
отдельно, может выполнить всю работу ?
РЕШЕНИЕ:
Производительность труда, то есть часть работы,
выполняемая в единицу времени (обозначим её через А),
и время, необходимое для выполнения всей работы (обозначим его через t), – взаимно обратные величины, то есть
Аt = 1.
Итак, первый рабочий может выполнить всю работу за 10
час, а второй – за 15 час.
Моторная лодка прошла 25 км по течению реки и 3 км против течения, затратив на весь путь 2 час. Какова скорость лодки в стоячей воде, если скорость течения реки равна 3 км/час ?
РЕШЕНИЕ:
Пусть x км/час
– скорость лодки в стоячей воде. Тогда скорость лодки по течению
(x + 3) км/час,
Значит, время, затраченное на весь путь, равно
По условию задачи на весь путь лодка затратила 2 час. Следовательно,
Решив это уравнение, найдём, что его корни
x1 = 2 и x2 = 12.
По смыслу задачи скорость лодки в стоячей воде должна быть больше скорости течения. Этому условию удовлетворяет второй корень – число 12 и не удовлетворяет первый.
ОТВЕТ: 12 км/час.
ЗАДАЧА:
Теплоход проплыл по течению речки 48 км и столько же против течения и затратил на весь путь 5 час. Определите скорость теплохода в стоячей воде, если скорость течения речки 4 км/час.
Скорость теплохода в стоячей воде принимаем за х (км/час). Тогда его скорость по течению речки будет х + 4 (км/час), а скорость против течения х – 4 (км/час). Значить, он пройдет по течению 48 км за
и против течения за
По условию задачи имеем:
После преобразования получим уравнение:
х2 – 96х – 80 = 0.
Его корни
х1 = 20, х2 = –4/5.
Тогда, скорость теплохода в стоячей воде была 20 км/час.
ЗАДАЧА:
За 4 дня общей работы двух тракторов с разными мощностями вспахано 2/3 колхозного поля. За сколько дней можно было б вспахать все поле каждым трактором отдельно, если первый трактор может вспахать всё поле на 5 дней раньше, чем второй ?
Роботу принимаем за единицу. Допустим, что вторым трактором можно вспахать всё поле за х дней, тогда первым трактором его можно вспахать за х – 5 дней. Значить, за 4 дня второй трактор вспашет
частину.
После преобразования это уравнение приобретает вид:
х2 – 17х + 30 = 0.
Его корни
х1 = 15, х2 = 2.
Второй корень не соответствует условию задачи, так как
2 – 5 = –3.
Поэтому, второй трактор может вспахать всё поле за 15 дней, а первый – за 10 дней.
ЗАДАЧА:
Набирая ежедневно на 3 страницы больше, чем планировалось,
оператор компьютерного набора закончил работу в объеме 60
страниц днем раньше срока. Сколько страниц набирал он каждый день ?
РЕШЕНИЕ:
12 + 3 = 15 (стр.).
ОТВЕТ: 15 страниц
ЗАДАЧА:
Во время строительства нового
театра бригада рабочих должна была смонтировать 420 зрительских мест. Задача была выполнена на
день раньше запланированного срока, поскольку ежедневно монтировали на 10
мест больше, чем было запланировано. Сколько мест монтировала бригада каждый
день ?
РЕШЕНИЕ:
60 + 10 = 70 (мест).
ОТВЕТ: 70 мест
ЗАДАЧА:
Катер прошел 15
км по течению реки и 4
км по озеру, потратив на весь путь 1 час.
Найдите собственную скорость катера, если скорость течения реки составляет 4
км/час.
РЕШЕНИЕ:
ОТВЕТ: 16
км/час
ЗАДАЧА:
После двух последовательных
повышений цены на одно и то же количество процентов цена стула выросла с 500 руб до 720 руб. На сколько процентов каждый раз повышали цену ?
РЕШЕНИЕ:
х = –220
не отвечает условию задачи.
ОТВЕТ: цену повышали на 20% каждый раз.
ЗАДАЧА:
Бассейн можно наполнить водой через две трубы. В течение 7 часов бассейн наполняли через первую трубу, а затем
открыли и вторую трубу. Через 2 часа после этого бассейн был наполнен. За сколько часов
можно наполнить бассейн через первую трубу, если для этого нужно на 4
часа больше, чем для того, чтобы наполнить бассейн через вторую трубу ?
РЕШЕНИЕ:
Уравнение:х = –1 не отвечает условию задачи. Поэтому вторая труба наполнит бассейн за 8 час, а первая за
8 + 4 = 12 (час).
ОТВЕТ: 12 час
ЗАДАЧА:
На путь, равный 18 км, велосипедист потратил времени на 1 час 48 мин меньше пешехода, поскольку за 1 час
проезжал на 9
км больше, чем проходил пешеход. Найдите скорость велосипедиста и скорость
пешехода.
РЕШЕНИЕ:
6 + 9 = 15 (км/час).
ОТВЕТ: 15 км/час, 6 км/час
ЗАДАЧА:
Турист проехал на велосипеде 2/3 всего пути, а остальное расстояние прошел
пешком. На велосипеде он ехал на 1 час 15 мин меньше, чем
шел пешком. Скорость движения туриста пешком на 8
км/ч меньше скорости его движения на
велосипеде. С какой скоростью турист двигался пешком, и с какой скорость он
ехал на велосипеде, если весь путь составлял 45
км ?
РЕШЕНИЕ:
12 – 8 = 4 (км/час).
ОТВЕТ: 4 км/час, 12 км/час
ЗАДАЧА:
Первый оператор может произвести компьютерный набор книги
на 6
дней быстрее, чем второй. Если первый оператор будет работать 3
дня, а затем его сменит второй и будет работать 9
дней, то будет выполнено 75% набора. За сколько дней может выполнить этот набор
каждый оператор ?
РЕШЕНИЕ:
18 – 6 = 12 (дней).
ОТВЕТ: 12 дней, 18 дней
ЗАДАЧА:
Расстояние от пункта А до пункта В по шоссе равно 120
км, а по железной дороге – 150
км. Автомобиль из пункта А выехал на 25
мин позже поезда и прибыл в пункт В на 35 мин раньше.
Найдите скорость автомобиля, если она на 20
км/час больше скорости поезда.
РЕШЕНИЕ:
25
мин + 35
мин = 1
час.
ОТВЕТ: 80 км/час
ЗАДАЧА:
Из города А в город В выехал велосипедист. Через 3
часа из города А выехал
мотоциклист, прибывший в город В одновременно с
велосипедистом. Найдите скорость мотоциклиста, если она на 45
км/час больше скорости велосипедиста, а
расстояние между городами А и В становит 60
км.
РЕШЕНИЕ:
15 + 45 = 60 (км/час).
ОТВЕТ: 60 км/час
ЗАДАЧА:
Турист проплыл на моторной лодке 30
км против течения реки и вернулся обратно
на плоту. Найдите скорость течения реки, если на плоту турист плыл на 3
часа дольше, чем на лодке, а собственная
скорость лодки составляет 15 км/час.
РЕШЕНИЕ:
ОТВЕТ: 5 км/час
ЗАДАЧА:
Велосипедист проехал из деревни на станцию и вернулся
назад. На обратном пути он увеличил скорость на 1
км/час по сравнению с движением на
станцию и израсходовал на этот путь на 2 мин меньше. С какой скоростью ехал велосипедист на
станцию, если расстояние между деревней и станцией составляет 8
км ?
РЕШЕНИЕ:
ОТВЕТ: 15 км/час
ЗАДАЧА:
Катер проходит 4 км против течения
реки и 15
км по течению за
такое же время, как нужно плоту, чтобы проплыть 2
км по этой реке. Найдите скорость
течения, если собственная скорость катера равна 18
км/ч.
РЕШЕНИЕ:
ОТВЕТ: 2 км/час
ЗАДАЧА:
Лодка проплыла 5 км по течению
реки и 3
км против течения, потратив на весь путь
40
мин. Скорость течения составляет 3 км/ч. Найдите скорость движения лодки по течению.
РЕШЕНИЕ:
Пусть скорость лодки в стоячей воде равна х км/час. Тогда его скорость по
течению – (х + 3) км/час,
а против течения – (х – 3) км/час.
5х – 15 + 3х + 9 = 2/3 (х2
– 9),
8х – 6 = 2/3 (х2
– 9),
24х – 18 = 2(х2 – 9),
12х – 9 = х2 – 9,
х2 – 12х = 0,
х1 = 0, х2 = 12,
х = 0 не отвечает условию задачи.
Поэтому, скорость движения по течению реки
12 + 3 = 15 км/час.
ОТВЕТ: 15 км/час
ЗАДАЧА:
Катер прошел 40 км по течению
реки и такое же расстояние против течения, потратив на путь против течения на 20
мин больше, чем на путь по течению. Найдите свою скорость катера, если скорость
течения реки составляет 3 км/час.
РЕШЕНИЕ:
- Урок 1. Линейные уравнения с одной переменной и целыми свободными членами
- Урок 2. Линейные уравнения с одной переменной и дробными свободными членами
- Урок 3. Применение правил определения неизвестного слагаемого, уменьшаемого и вычитаемого для решения задач
- Урок 4. Применение правил определения неизвестного множителя для решения задач
- Урок 5. Решение уравнений, сводимых к линейным
- Урок 6. Решение уравнений с переменной в знаменателе
- Урок 7. Применение правил опреднления делимого и делителя для решения задач
- Урок 8. Линейные уравнения с двумя переменными
- Урок 9. Решение линейных уравнений с помощью графиков
- Урок 10. Линейные уравнения с параметрами
- Урок 11. Системы уравнений первой степени с двумя неизвестными
- Урок 12. Решение систем уравнений способом подстановки
- Урок 13. Решение систем уравнений способом алгебраического сложения
- Урок 14. Решение линейных систем уравнений с помощью графиков
- Урок 15. Решение задач с помощью систем уравнений первой степени
- Урок 16. Системы линейных уравнений с тремя неизвестными
- Урок 17. Полное квадратное уравнение общего вида
- Урок 18. Приведённое квадратное уравнение
- Урок 19. Теорема Виета
- Урок 20. Неполные квадратные уравнения
- Урок 21. Решение квадратных уравнений выделением квадрата двучлена
- Урок 22. Графический способ решения квадратных уравнений
- Урок 23. Квадратный трёхчлен
- Урок 24. Квадратные уравнения с параметрами
- Урок 25. Дробные рациональные уравнения
- Урок 27. Уравнение окружности
- Урок 28. Системы уравнений второй степени с двумя неизвестными
- Урок 29. Решение задач с помощью систем уравнений второй степени
- Урок 30. Пересечение прямой и окружности
- Урок 31. Решение нелинейных систем уравнений с помощью графиков
- Урок 32. Системы уравнений с параметрами
- Урок 33. Уравнения высших стапеней
- Урок 34. Решение уравнений способом замены
- Урок 35. Решение систем уравнений способом замены
- Урок 36. Задачи на нахождение чисел
- Урок 37. Задачи на нахождение цифр
- Урок 38. Решение задач на смешивание с помощью уравнений
- Урок 39. Решение задач на смешивание с помощью систем уравнений
- Урок 40. Иррациональные уравнения
- Урок 41. Уравнения с модулем
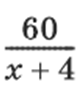































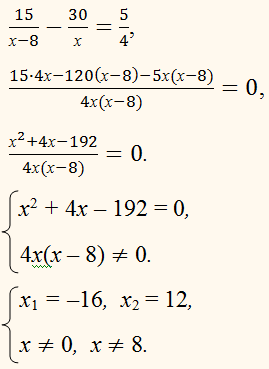
















Комментариев нет:
Отправить комментарий