Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ВЕКТОРОВ
или посмотрите
ВИДЕО УРОК
1. На рисунке изображён ромб АВСD, у которого
АВ = 2 см,
б) 8 cм2;
в) 6 cм2;
г) 4 cм2.
2. С помощью скалярного произведения векторов найти угол при вершине А параллелограмма АВСD, построенного на векторах
б) ≈ 76°;
в) ≈ 68°;
г) ≈ 70°.
3. Вершинами пирамиды служат точки
А(1; 2, 3), B(0; –1, 1),
C(2; 5, 2), D(3; 0, –2).
Вычислить объём пирамиды.
а) 5 ед. объёма;
б) 3 ед. объёма;
в) 6 ед. объёма;
г) 4 ед. объёма.
4. В пространстве задан треугольник
координатами своих вершин
А1(1; 1; 1),
А2(3; 0; 0),
А3(2; 3; 7).
Найти угол между сторонами
А1А2 и А1А3.
а) ≈
116°;
б) ≈ 112°;
в) ≈
110°;
г) ≈
100°.
5. Треугольник задан своими вершинами:
А(–1; 0),
В(3; 2),
С(5; –1).
Найти проекцию стороны АВ на сторону АС.
а) ≈ 3,62 ед.;
б) ≈
3,68 ед.;
в) ≈
3,58 ед.;
г) ≈
3,66 ед.
6. Треугольник
задан своими вершинами:
А(–1; 0),
В(3; 2),
С(5; –1).
Найти проекцию стороны АС на сторону АВ.
а) ≈
4,82 ед.;
б) ≈
4,98 ед.;
в) ≈
4,88 ед.;
г) ≈ 4,92 ед.
7. Найдите в градусах внешний угол при
вершине А треугольника АМК, если
А(2; –2; –3),
М(4; –2; –1),
К(2; 2; 1).
а) 130°;
б) 110°;
в) 120°;
г)
100°.
б) 8;
в) 4;
г) –4.


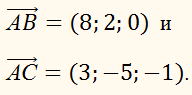










Комментариев нет:
Отправить комментарий