Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
ДЕЙСТВИЯ НАД ВЕКТОРАМИ В ПРОСТРАНСТВЕ
или посмотрите
ВИДЕО УРОК
1. При каком значении k векторы
перпендикулярны ? а) 3;
б) –3;
в) 4;
г) –4.
б) cos α = 1/3, cos β
= 2/3, cos γ = 2/3;
в) cos α = 1/3, cos β
= 1/3, cos γ = 2/3;
г) cos α = 1/3, cos β
= 1/3, cos γ = 1/3.
3.
Даны точки
А(5; –6; 7) и В(8; –2; 7).
б) 8;
в) 4;
г) 5.
а) да;
б) ;
в) нет;
г) .
а) 1;
б) 3;
в) 2;
г) 0.
б) ;
в) да;
г) .
б) ;
в) да;
г) .
б) 10;
в) 12;
г) 9.
а) 4,5;
б) 2;
в) 17;
г) 68.
б) cos α = 13/15;
в) cos α = 12/13;
г) cos α = 11/13.
б) cos α = 0,1√͞͞͞͞͞3;
в) cos α = 0,1√͞͞͞͞͞5;
г) cos α = 0,3√͞͞͞͞͞3.
б) 2;
в) 0;












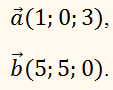


Комментариев нет:
Отправить комментарий