Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
НЕРІВНІСТЬ З МОДУЛЕМ
або
ВИДЕО УРОК
1. Розв’яжіть нерівність:
|x – 2| <
0.
а) (0; 2);
б) (–∞; +∞);
в) (–∞; 2);
г) розв’язків
немає.
2. Розв’яжіть
нерівність:
|x –1| ≥
– 2.
а) [1; +∞);
б) (–∞; +∞);
в) [–2; 2];
г) розв’язків
немає.
3. Скільки існує цілих значень х,
при яких є правильною нерівність ?
|х| ≤ 34.
а) 68;
б) 34;
в) 69;
г) 35.
4. Знайти
від’ємні цілі числа, які є розв’язками нерівності:
|х| ≤ 3.
а) 3; 2; 1;
б) –2; –1;
в) –3; –2; –1;
г) –3; –2; –1; 0.
5.
Розв’яжіть нерівність:
|х| > –2.
а) х > –2;
б) х – будь-яке число;
в) х >
0;
г) х > 2.
6. Який
з проміжків є множиною розв’язків нерівності ?
|2 – х| < 3.
а) (–∞; –1) ∪ (5; +∞);
б) (–1; 5);
в) (–1; +∞);
г) (–5; +∞).
7. У якому з випадків на
малюнку зображено множену розв’язків нерівності ?
8. Розв’яжіть нерівність:
|х – 3| < 5.
а) (–8; 8);
б) (–2; 8);
в) (–2; 2);
г) (–5; 0).
9. Розв’яжіть нерівність:
|2х – 1| > 5.
а) (–∞; –3) ∪ (2; +∞);
б) (–∞; –2) ∪ (2; +∞);
в) (–∞; –3) ∪ (3; +∞);
г) (–∞; –2) ∪ (3; +∞).
б) (–4/3; –1/2];
в) [–4/3; –1/2];
г) [–4/3; –1/2).
11.
Розв’яжіть
нерівність:
|2 + х| ≥
|х|.
а) x ≥ 1;
б) x
≤ –1;
в) x
≥ –1;
г) x ≤ 1.
12.
Розв’яжіть
нерівність:
|х – 3| + |х – 4| > 1.
а) (–∞; 2) ∪ (4; +∞);
б) (–∞; 3) ∪ (4; +∞);
в) (–∞; 3) ∪ (3; +∞);
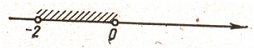



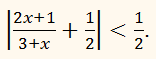
Комментариев нет:
Отправить комментарий