Задание 4. График функции у = aх2 + bx + c

Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока 

График функции  у = aх² + bx + c

 1. Постройте график функции:

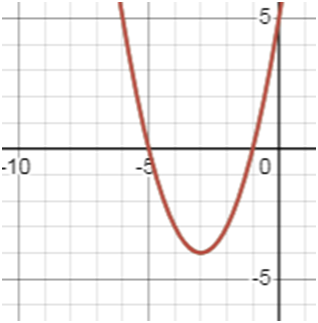
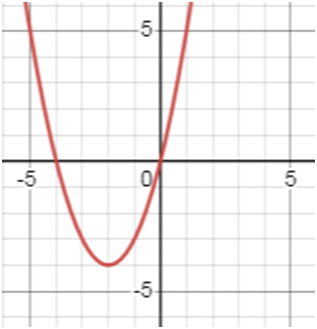
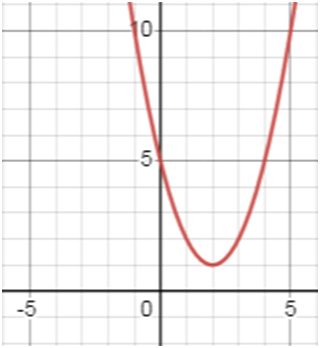
у = х² + 6х + 5.

Пользуясь графиком, найдите промежуток убывания функции.

 а)

убывает на промежутку – [1; +∞);

б)
убывает на промежутку – (–∞; –3];

 в)

убывает на промежутку – [3; +∞);

 г)

убывает на промежутку – (–∞; –1].

 2. Найдите ординату вершины параболы, фрагмент которой изображён на рисунку.

                                              у

                                                                            

 а)  –1,5;

 б)  –2;

 в)  0;

 г)  –1.

 3. Постройте график функции:

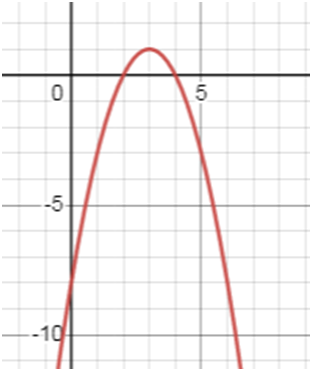
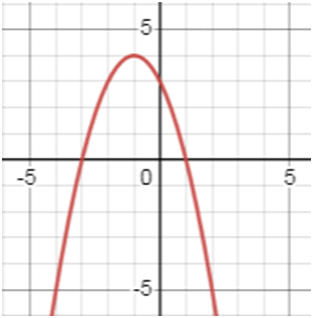
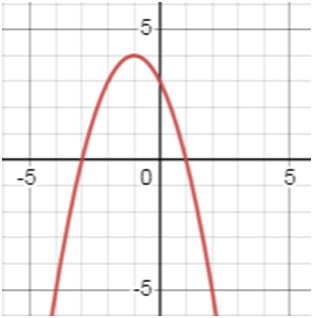
у = 3 + 2х – х².

Пользуясь графиком, найдите область значений функции;

 а)
область значений функции – (–∞; 4];

 б)

область значений функции – [–9; +∞);

 в)

область значений функции – (–∞; 1];

 г)

область значений функции – [–5; +∞);

 4. Постройте график функции:

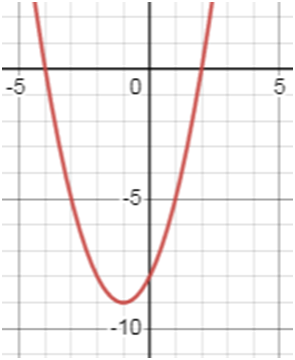
у = х² + 2х – 8.

Пользуясь графиком, найдите при каких значениях  х  функция приобретает отрицательные значения.

 а)

функция приобретает отрицательные значения

х ∈ (–∞; 2) ∪ (4; +∞)

 б)

функция приобретает отрицательные значения

х ∈ (–∞; –1) ∪ (3; +∞);

в)
функция приобретает отрицательные значения

х ∈ (–4; 2);

 г)

функция приобретает отрицательные значения

х ∈ (–5; –1).

 5. Постройте график функции:

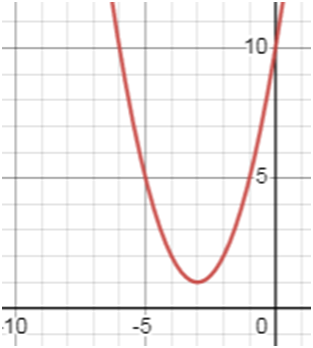
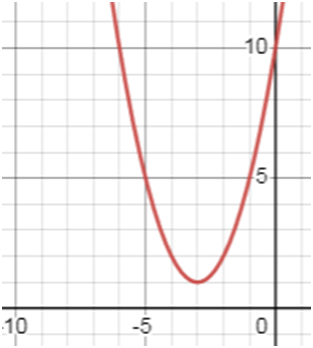
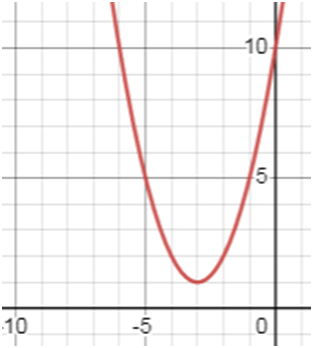
у = х² + 6х + 10.

Пользуясь графиком, найдите промежуток убывания функции.

 а)
убывает на промежутку – (–∞; –3];

б)
убывает на промежутку – [–3; +∞);

в)
убывает на промежутку – [–1; +∞);

г)
убывает на промежутку – (–∞; –2].

 6. Постройте график функции:

у = –х² – 6х – 8.

Пользуясь графиком, найдите область значений функции;

 а)
область значений функции – [1; +∞);

 б)
область значений функции – [–4; +∞);

 в)
область значений функции – (–∞; 1];

 г)
область значений функции – (–∞; 4].

 7. Постройте график функции:

у = 3 – 2х – х².

Пользуясь графиком, найдите промежуток убывания функции.

 а)
убывает на промежутку – (–∞; –2];

 б)
убывает на промежутку – [–1; +∞),

в)

убывает на промежутку – [–3; +∞);

 г)

убывает на промежутку – (–∞; –3],

 8. Постройте график функции:

у = х² + 4х.

Пользуясь графиком, найдите промежуток убывания функции;

 а)

убывает на промежутку – [–3; +∞);

 б)
убывает на промежутку – (–∞; –3];

в)
убывает на промежутку – [–1; +∞),

г)
убывает на промежутку – (–∞; –3].

 9. Постройте график функции:

у = –х² + 4х – 3.

Пользуясь графиком, найдите промежуток возрастания функции.

 а)
возрастает на промежутку – [2; +∞);

 б)
возрастает на промежутку – (–∞; 2];

 в)
возрастает на промежутку – (–∞; 3];

 г)
возрастает на промежутку – (–∞; 4].

10. Постройте график функции:

у = –х² + 8х – 12.

Пользуясь графиком, найдите, при каких значениях  х  функция приобретает положительные значения.

 а)
функция приобретает положительные значения

х ∈ (1; 3);

 б)
функция приобретает положительные значения

х ∈ (1; 5)

 в)
функция приобретает положительные значения

х ∈ (–∞; +∞);

 г)
функция приобретает положительные значения

х ∈ (2; 6).

11. Постройте график функции:

у = х² – 4х + 5.

Пользуясь графиком, найдите, при каких значениях  х  функция приобретает отрицательные значения.

 а)
отрицательных значений нет;

б)
функция приобретает отрицательные значения

х ∈ (–∞; 1) ∪ (5; +∞);

 в)
функция приобретает отрицательные значения

х ∈ (–∞; 2) ∪ (6; +∞);

 г)
функция приобретает отрицательные значения

х ∈ (–∞; 1) ∪ (3; +∞).

12. Постройте график функции:

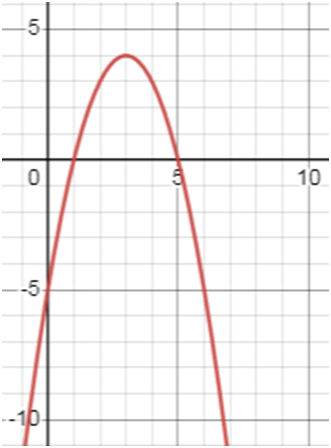
у = –х² + 6х – 5.

Пользуясь графиком, найдите, при каких значениях  х  функция приобретает положительные значения.

 а)
функция приобретает положительные значения

х ∈ (1; 3);

 б)
функция приобретает положительные значения

х ∈ (2; 6);

 в)
функция приобретает положительные значения

х ∈ (1; 5);

 г)
функция приобретает положительные значения

х ∈ (–∞; +∞).

Задания к уроку 27

• Задание 1
• Задание 2
• Задание 3