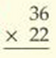Before proceeding to the solution of examples and problems be sure to read the theoretical part of the lesson
Multiplying natural numbers
1. 28 books. 88 pages in each book. How many pages in all books?
а) 148040;
b) 147040;
c) 147060;
d) 147140.
b) 147040;
c) 147060;
d) 147140.
2. A video game company can fit 535
boxes of games into a truck. If the company has 47
full trucks, how many games does it have in total?
а) 25145;
b) 26145;
c) 25245;
d) 25155.
b) 26145;
c) 25245;
d) 25155.
3. Each day, 1,035
new apps are uploaded to a web server. After 28
days, how many apps would have been uploaded?
а) 28780;
b) 26980;
c) 28970;
d) 28980.
b) 26980;
c) 28970;
d) 28980.
4. The zookeeper gave 2
bags of peanuts to an elephant. There were 12
peanuts in each bag. How many peanuts did the zookeeper give to the elephant?
а) 14; b) 6;
c) 24; d) 26.
c) 24; d) 26.
5. Ariel earns money by mowing lawns in his neighborhood.
If he can mow 3 lawns in an hour, how many lawns can he mow working 30
hours a week?
а) 60; b) 90;
c) 33; d) 99.
c) 33; d) 99.
6. Winona is tracking the amount of water that the people
of her town use during the summer months. She calculates that 47,005
gallons of water are used every day. If Winona tracks the water usage for 112
days, how much water will be used during that time?
а) 5264650;
b) 5264565;
c) 5264555;
d) 5264560.
b) 5264565;
c) 5264555;
d) 5264560.
7. Basil launched his website this year. During the first three months of
operation, his site recorded 835,884 hits. If he maintains that same monthly average, how
many hits should he expect by the end of the fifteenth month?
а) 4179420;
b) 12538460;
c) 12538260;
d) 4179620.
b) 12538460;
c) 12538260;
d) 4179620.
8. Maria did 25 sets of 15
jumping jack, 18 sets of 20 sit-ups, 21
sets of 12 push-ups, and 16
sets of 10 pull-ups. How many times did Maria do each exercise?
а) 330
jumping jacks, 480 sit-ups,
192 push-ups, 220 pull-ups;
b) 375 jumping jacks, 360 sit-ups,
252 push-ups, 160 pull-ups;
c) 480
jumping jacks, 340 sit-ups,
180 push-ups, 190 pull-ups;
d) 225
jumping jacks, 520 sit-ups,
312 push-ups, 200 pull-ups.
9. Al did 22
sets of 15 jumping jack, 24
sets of 20 sit-ups, 16 sets of 12
push-ups, and 22 sets of 10 pull-ups. How
many times did Maria do each exercise?
а) 480
jumping jacks, 340 sit-ups,
180 push-ups, 190 pull-ups;
b) 375
jumping jacks, 360 sit-ups,
252 push-ups, 160 pull-ups;
c) 225 jumping jacks, 520 sit-ups,
312 push-ups, 200 pull-ups;
d) 330 jumping jacks, 480 sit-ups,
192 push-ups, 220 pull-ups;
10. Hannah did 32
sets of 15 jumping jack, 17
sets of 20 sit-ups, 15 sets of 12
push-ups, and 19 sets of 10 pull-ups. How
many times did Maria do each exercise?
а) 225
jumping jacks, 520 sit-ups,
312 push-ups, 200 pull-ups;
b) 375
jumping jacks, 360 sit-ups,
252 push-ups, 160 pull-ups;
c) 480 jumping jacks, 340 sit-ups,
180 push-ups, 190 pull-ups;
d) 330 jumping jacks, 480 sit-ups,
192 push-ups, 220 pull-ups.
11. Jorge did 15
sets of 15 jumping jack, 26
sets of 20 sit-ups, 26 sets of 12
push-ups, and 20 sets of 10 pull-ups. How
many times did Maria do each exercise?
а) 480
jumping jacks, 340 sit-ups,
180 push-ups, 190 pull-ups;
b) 225 jumping jacks, 520 sit-ups,
312 push-ups, 200 pull-ups;
c) 330
jumping jacks, 480 sit-ups,
192 push-ups, 220 pull-ups;
d) 375
jumping jacks, 360 sit-ups,
252 push-ups, 160 pull-ups.
12. A video game
company can fit 535 boxes of games into a truck. If the company has 47
full trucks, how many games does it have total?
c) 24145; d) 25245.