Урок 3. Об'єм похилої призми

вторник, 6 февраля 2018 г.

Урок 3. Об'єм похилої призми

Похила призма рівновелика такій прямій призмі, основа якої дорівнює перпендикулярному перерізу похилої призми, а висота – її бічному ребру.

На рисунку зображені ABCDA₁B₁C₁D₁ – похила призма, а A'B'C'D'A₁'B₁'C₁'D₁' – пряма призма, основа якої A'B'C'D', перпендикулярна до бічних ребер похилої призми, а висота (бічне ребро) A' A₁'= AA₁ = H. У цьому випадку

Об'єм похилої призми дорівнює добуткові площі основи на висоту:

де S_осн – площа основи ABCDE, а H = OO₁ – висота.

Якщо у похилій призмі проведено переріз, перпендикулярний до бічних ребер, що перетинає всі бічні ребра (переріз KML на малюнку).

Тоді об'єм призми V можна знайти за формулою:

V = S_пер× l,

де S_пер – площа перерізу, l – довжина бічного ребра.

Якщо в похилій призмі бічне ребро утворює однакові кути із сторонами основи, які виходять з його одного кінця, то проекція ребра на площину основи є бісектрисою відповідного кута основи.

Якщо в похилій призмі дві суміжні бічні грані утворюють однакові двогранні кути з основою, то проекція на основу бічного ребра, яке належить ліній перетину двох граней вказаних двогранних кутів, є бісектрисою кута основи.

ЗАДАЧА:

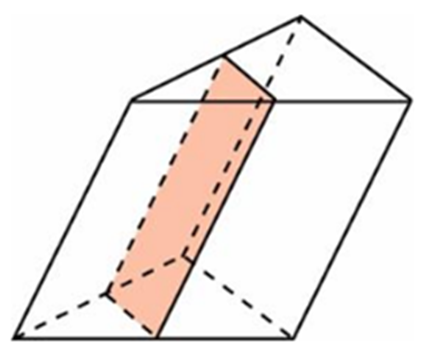
Через середню лінію основи трикутної похилої призми проведено площину, паралельну бічному ребру. Об'єм відсіченої трикутної призми дорівнює 5. Знайдіть обсяг вихідної призми.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.

Площа основи відсіченої частини менша від площі основи всієї призми в 4 рази (так як і висота і основа трикутника зменшилися в 2 рази). Висоти обох частин призми однакові, тому обсяг відсіченої частини в 4 рази менше обсягу цілої призми, отже, обсяг вихідної призми дорівнює

5 ∙ 4 = 20.

ЗАДАЧА:

У похилій трикутній призмі площа однієї з бічних граней становить m², а віддаль її від протилежного ребра дорівнює 2а. Знайти об'єм призми.

Нехай РМN – перпендикулярний переріз призми

АС₁ і МL ⊥ РN,

тоді за умовою задачі

МL = 2а, а РN × ВВ₁ = m².

Відомо, що об'єм призми

V = BB₁ × S_PMN,

або

V = ¹/₂× PN × ML × BB₁

= ¹/₂(PN × BB₁) × ML

= ¹/₂m² × 2a = am².

ВІДПОВІДЬ:

V = am².

ЗАДАЧА:

Бічне ребро похилої трикутної призми дорівнює 6 см, дві бічні грані її взаємно перпендикулярні та їх площі дорівнюють 24 см²і 30 см². Знайти об'єм призми.

Нехай маємо похилу трикутну призму АВСА₁В₁С₁ з бічним ребром А₁А = 6 см, площини бічних граней АСС₁А₁ та ВСС₁В₁ якої взаємно перпендикулярні,

Проведемо перпендикулярний переріз А'В'С'. Тоді:

Оскільки (A'B'C') ⊥ C₁C і площини A₁C₁C та B₁C₁C взаємно перпендикулярні, то

∠ A'B'C'= 90°.

Отже,

і шуканий об'єм

ВІДПОВІДЬ: 60 см³.

ЗАДАЧА:

У похилій трикутній призмі основою є правильний трикутник. Одна з вершин верхньої основи трикутника проектується в нижній центр. Бічні ребра призми складають із площиною основи кут 45°. Знайдіть обсяг призми, якщо її висота дорівнює 4.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.

Проекція О вершини верхньої основи А₁ – центр нижньої та є центром описаної біля нижньої основи кола. Відрізок А₁О – висота призми. АО – катет прямокутного трикутника АОА₁.

АО = А₁О : tg 45° = 4.

АО – радіус R описаного кола.

R = а : √͞͞͞͞͞3,

а = R∙ √͞͞͞͞͞3 = 4√͞͞͞͞͞3.

Площа рівностороннього трикутника знаходимо за такою формулою:

V_призмы = S_ABC ∙ A₁O.
V_призмы = 12√͞͞͞͞͞3 ∙ 4 = 48√͞͞͞͞͞3.

Завдання до уроку 3

Інші уроки:

Уроки математики и физики для школьников и родителей

вторник, 6 февраля 2018 г.