Задание 2. Решение неравенств с помощью графиков

Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока 

РЕШЕНИЕ НЕРАВЕНСТВ С ПОМОЩЬЮ ГРАФИКОВ

или посмотрите

ВИДЕО УРОК

 1. На рисунку изображён график функции

у = х² + 2х + 1

Назовите множество решений неравенства:

х² + 2х + 1 < 0.

 а)  (–∞; –1] ∪ [–1; +∞);     

 б)  –1;     

 в)  (–∞; –1) ∪ (–1; +∞);     

 г)  ∅.

 2. На рисунку изображён график функции

 y = f(x),

у которого область определения – множество действительных чисел. Пользуясь графиком, найдите множество решений неравенства

y = f(x) ≥ 0.

 а)  [–2,5; 1];     

 б)  (–2,5; 1) ∪ (4; +∞);     

 в)  [–2,5; 1] ∪ [4; +∞);     

 г)  (–2,5; 1).

 3. На рисунку изображён график квадратичной функции

 y = f(x),

который пересекает ось абсцисс в точках

(–2; 0)  и  (1; 0).

Найдите множество решений неравенства

х ∙ f(x) < 0.

 а)  (–2; 1);     

 б)  (–∞; 0);     

 в)  (–∞; –2) ∪ (0; 1);     

 г)  (–2; 0) ∪ (1; +∞).

 4. На рисунку изображён график квадратичной функции

 y = f(x),

который пересекает ось абсцисс в точках

(1; 0)  и  (3; 0).

Найдите множество решений неравенства

х ∙ f(x) ˃ 0.

 а)  (1; 3);     

 б)  (–∞; 0) ∪ (1; 3);     

 в)  (0; 1) ∪ (1; 3);     

 г)  (–∞; 1).

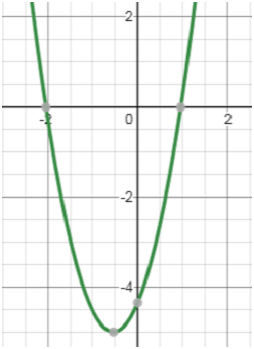
 5. На рисунке изображён график функции

у = х² – 2х – 3.

Назовите множество решений неравенства

х² – 2х – 3 ≥ 0.

 а)  (–∞; –1) ∪ (3; +∞);     

 б)  (–∞; –1] ∪ (3; +∞);     

 в)  (–∞; –1] ∪ [3; +∞);     

 г)  (–∞; –1) ∪ [3; +∞).

 6. На рисунке изображён график функции

у = х² + 2х + 1.

Назовите множество решений неравенства:

х² + 2х + 1 ≥ 0.

 а)  (–∞; +∞);     

 б)  –1;     

 в)  (–∞; –1) ∪ (–1; +∞);     

 г)  ∅.

 7. На рисунке изображён график функции

у = х² – 6х + 5.

Назовите множество решений неравенства:

х² – 6х + 5 ≤ 0.

 а)  (1; 5];     

 б)  [1; 5];     

 в)  (1; 5);     

 г)  [1; 5).

 8. На рисунке изображён график функции

у = 6х – х².

Назовите множество решений неравенства:

6х – х² ≤ 0.

 а)  (–∞; 0) ∪ (6; +∞);     

 б)  (–∞; 0) ∪ [6; +∞);     

 в)  (–∞; 0] ∪ [6; +∞);     

 г)  (–∞; 0] ∪ (6; +∞).

 9. На рисунке изображён график функции

у = х² + 4х.

Назовите множество решений неравенства:

х² + 4х ≤ 0.

 а)  (–∞; –4] ∪ (0; +∞);     

 б)  (–∞; –4) ∪ (0; +∞);     

 в)  (–∞; –4) ∪ [0; +∞);     

 г)  (–∞; –4] ∪ [0; +∞).

10. На рисунке изображён график функции

у = –х² + 8х – 12.

Назовите множество решений неравенства:

–х² + 8х – 12 ≥ 0.

 а)  (–∞; 2) ∪ (6; +∞);     

 б)  [2; 6];     

 в)  (–∞; 2] ∪ [6; +∞);     

 г)  (2; 6).

11. На рисунке изображён график функции

у = –4х – х².

Назовите множество решений неравенства:

–4х – х² ≥ 0.

 а)  (–∞; –4) ∪ (0; +∞);     

 б)  (–4; 0);     

 в)  (–∞;–4] ∪ [0; +∞);     

 г)  [–4; 0].

12. На рисунке изображён график функции

у = х² – 4х – 5.

Назовите множество решений неравенства:

х² – 4х – 5 ≤ 0.

 а)  (–∞; –1) ∪ (5; +∞);     

 б)  (–1; 5);     

 в)  (–∞;–1] ∪ [5; +∞);     

 г)  [–1; 5].

Задания к уроку 10

• Задание 1
• Задание 3