ВИДЕО УРОК
Неравенства вида
где Рn(x); Qm(x) – многочлены соответственно степеней n и m, т. е.Рn(x) = anxn + an-1xn-1 + … + a1x + a0;
Qm(x) = bmxm
+ bm-1xm-1 + … + b1x + b0;
Решение рациональных неравенств вида(вместо знака ˃ может быть и любой другой знак неравенства), где Рn(x); Qm(x) – многочлены, основано на следующем рассуждении.
Рассмотрим выражение:где a < b < c < d.
Если x ˃ d, то
каждый из множителей
x – a, x – b, x – c, x – d
положителен и,
следовательно, на промежутке (d;
+∞) имеем
h(x) ˃ 0.
Если c < x
< d, то x – d < 0, а остальные
множители по-прежнему положительны. Значит, на интервале (c; d) имеем h(x) <
0.
На тех промежутках,
где эта кривая проходит выше координатной прямой, выполняется неравенство h(x) ˃ 0,
на тех же промежутках, где кривая проходит ниже прямой, имеем h(x) < 0.
a1, a2, …, an, b1, b2, …, bk
попарно различны.
Изменение знаков функции y = f(x) можно также
иллюстрировать с помощью кривой знаков, которую чертят справа налево, начиная
сверху, и проводят через все отмеченные на координатной прямой точки
a1, a2, …, an, b1, b2, …, bk.
На этом основан
метод промежутков, который с успехом применяется для решения рациональных
неравенств.
Рn(x) ×Qm(x) ˃ 0 (Рn(x)×Qm(x) < 0).
А × В ˃ 0.
Поэтому строгое
дробное неравенство всегда можно заменить равносильным ему целым алгебраическим
неравенством.
(x2 – 3x – 5)(3x2 + 2x – 1) ˃ 0,
так как эти
неравенства равносильны (эквивалентны).
Для того чтобы
решить неравенство
Рn(x)×Qm(x) ˃ 0,
необходимо разложить
многочлены
Рn(x) и Qm(x)
на множители:
где c1, c2, …, cn; k1, k2, … , kn – некоторые постоянные,а x1, x2, … , xn – корни уравнения
Рn(x) = 0.
Множеством решений
нестрогого неравенства
Рn(x)×Qm(x) ≥ 0 (Рn(x)×Qm(x) ≤ 0)
является
объединением двух множеств: множества решений строгого неравенства
Рn(x) ×Qm(x) ˃ 0 (Рn(x)×Qm(x) < 0)
и множества решений
уравнения
Рn(x) ×Qm(x) = 0.
ПРИМЕР:
х ˃ –1/2, х ˃
2/3, то
есть
х ˃ 2/3.
Из второй системы находим:
х < –1/2, х
< 2/3, то
есть
х < –1/2.
В итоге получили следующие решения заданного
неравенства:
х < –1/2, х ˃
2/3.
ОТВЕТ:
х < –1/2, х ˃
2/3
ПРИМЕР:
– если числитель меньше или равен нулю, а знаменатель
больше нуля;
– если числитель больше или равен нулю, а знаменатель меньше
нуля;
х ≤ 6, х ˃
7/2, то
есть
7/2 < х ≤ 6.
Из второй системы находим:
х ≥ 6, х
< 7/2,
то есть система не имеет решений.
Значит, множество решений заданного неравенства
есть промежуток:
(7/2; 6].
ПРИМЕР:
Данное неравенство равносильно
(х + 3)(х – 2)(х – 5) < 0.
Корни многочлена
(х + 3)(х – 2)(х – 5)
равны:
–3,
2, 5.
–∞ < х < –3 и
–∞ < х < –3, 2 < х < 5
ПРИМЕР:
x2 + 3x + 9 = 0 и
x2 – 2x + 4 = 0
отрицательны
(D1 = –27 < 0 и D2 = –12 < 0);
следовательно, они решений не имеют.
Отсутствие решений означает, что квадратные трёхчлены на
множители не раскладываются и на всём промежутке изменения х имеют постоянный знак, совпадающий со знаком
старшего члена (в нашем случае <<+>>).
Умножим и разделим исходное неравенство на положительные
выражения
x2 + 3x + 9 = 0 и
x2 – 2x + 4 = 0.
(х – 3)(х + 2) < 0.
–2 < х ≤ 3.
ОТВЕТ: (–2; 3]
ПРИМЕР:
Линейная функция х – а меняет знак при
переходе через точку а, причём правее точки
а эта
функция положительна, а левее точки а – отрицательна.
Отметив на числовой оси точки
–3,
–1, 2, 4,
При переходе через каждую из отмеченных точек один и
только один из этих множителей меняет знак, и поэтому знак дроби каждый раз
меняется. Учитывая это, расставим знаки дроби (смотрите рисунок). Итак, множество решений – объединение
следующих интервалов:
(–∞;
–3), (–1; 2), (4; +∞).
ОТВЕТ:
х < –3, –1 < х < 2, х ˃ 4
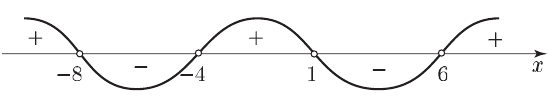
ПРИМЕР:
ОТВЕТ:
–8 ≤ х < –4, 1 ≤ х < 6
ПРИМЕР:
(х – 3) и (х + 1),
которые не могут равняться 0.
Первое неравенство имеет решение
х < –1 и х
˃ 3.
Решаем методом интервалов второе неравенство, его решение
–4 ≤ х < –1,
3 < х ≤ 4.
ПРИМЕР:
Квадратный трёхчлен
2х2 – 5х – 3
имеет корни
х = –1/2 и
х = 3.
Поэтому
2х2 – 5х – 3 = 2(х + 1/2)( х – 3).
Квадратный трёхчлен
3х2 – 4х + 2
принимает положительные значения при всех х ∈ R, так как его дискриминант
D =
16
– 24 < 0,
а старший коэффициент положителен.
Обозначим левую часть неравенства через Р(х).
Функция Р(х) не определена при
х = 7/3 и х = 2
и меняет знак при переходе через точки
(х + 1/2)( х – 1)(х – 7/3)( х – 3) ˃ 0.
Применяя метод интервалов, находим все решения исходного
неравенства с учётом того, что числа
–1/2, 1, и 3
принадлежат множеству решений неравенства, а число 2 не принадлежит этому множеству.
ОТВЕТ:
х ≤ –1/2, 1 ≤ х < 2,
2 < х < 7/3, х ≥
3
ПРИМЕР:
–5 < х <
–1, х
˃ 1.
ОТВЕТ:
–5 < х <
–1, х
˃ 1
ПРИМЕР:
Изменение знаков функции
х < –5,
–√͞͞͞͞͞2 < х < –5/4,
3/2 < х < √͞͞͞͞͞3.
Это решения исходного неравенства.
ОТВЕТ:
х < –5,
–√͞͞͞͞͞2 < х < –5/4,
3/2 < х < √͞͞͞͞͞3
- Урок 1. Числовые неравенства
- Урок 2. Свойства числовых неравенств
- Урок 3. Сложение и умножение числовых неравенств
- Урок 4. Числовые промежутки
- Урок 5. Линейные неравенства
- Урок 6. Системы линейных неравенств
- Урок 7. Нелинейные неравенства
- Урок 8. Системы нелинейных неравенств
- Урок 10. Решение неравенств с помощью графиков
- Урок 11. Неравенства с модулем
- Урок 12. Иррациональные неравенства
- Урок 13. Неравенства с двумя переменными
- Урок 14. Системы неравенств с двумя переменными
- Урок 15. Приближённые вычисления
- Урок 16. Абсолютная и относительная погрешность







































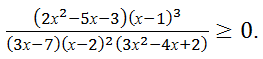
















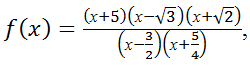

Комментариев нет:
Отправить комментарий