ВИДЕО УРОК
Что такое первообразная и как она считается ?
ПРИМЕР:
Найдём производную:
f(x) = x3.
Находим её, пользуясь формулой:
Откуда
Это и есть определение первообразной.
Аналогично запишем и такое выражение:
Обобщим это правило и выведем следующую формулу:
При n = –1 первообразная функция определяется следующим образом:
Учитывая, что
а производная
Первообразной функции называется такая функция, производная которой равна исходной функции.
Функция
y = F(x)
называется первообразной функции
y = f(x)
на промежутке Х, если для любого х ∈ Х выполняется равенство:
F(x) = f(x).
Таблица первообразных функций.
К каждому выражению в правой части таблицы необходимо прибавить константу.
Правила нахождения первообразных функций.
1. Первообразная функция суммы (разности) равна сумме (разности) первообразных функций.
F(x + у) = F(x) + F(у),
F(x – у) = F(x) – F(у).
ПРИМЕР:
Найти первообразную для функции
у = 4х3 + cos x.
РЕШЕНИЕ:
Первообразная суммы равна сумме первообразных, тогда надо найти первообразную для каждой из представленных функций.
f(x) = 4x3, F(x) = x4.
f(x) = cos x, F(x) = sin x.
Тогда первообразная исходной функции будет
у = х4 + sin x
или любая функция вида
у = х4 + sin x + C.
2. Если F(x) – первообразная для f(x), то
k F(x)–
первообразная для функции k f(x).
(Коэффициент можно выносить за функцию).
ПРИМЕР:
Найти первообразную для функции
у = 8 sin x.
РЕШЕНИЕ:
Первообразной для sin x служит минус cos x. Тогда первообразная исходной функции примет вид:
у = –8 cos x.
ПРИМЕР:
Найти первообразную для функции
у = 3x2 + 4х + 5.
РЕШЕНИЕ:
Первообразной для x2 служит
Первообразной для x служит
Первообразной для 1 служит x.
Тогда первообразная исходной
функции примет вид:
у = x3 + 2x2 + 5 x.
3. Если y = F(x) – первообразная для функции
y = f(x),
то первообразная для функции
y = f(kx + m)
служит функция
y = 1/k F(kx + m).
ПРИМЕР:
Найти первообразную для функции
у = cos (7x).
РЕШЕНИЕ:
Первообразной для cos x служит sin x. Тогда первообразная для функции
cos (7x)
будет функция
ПРИМЕР:
Найти первообразную для функции
у = sin x/2.
РЕШЕНИЕ:
Первообразной для sin x служит минус cos x. Тогда первообразная для функции
у = sin x/2
будет функция
ПРИМЕР:
Найти первообразную для функции
у = (–2х + 3)3.
РЕШЕНИЕ:
Первообразной для x3 служитТогда первообразная для исходной функции
у = (–2х + 3)3.
будет функция
ПРИМЕР:
Сначала упростим выражение в степени:
Первообразной экспоненциальной функции является сама экспоненциальная функция. Первообразной исходной функции будет:
Если y = F(x) – первообразная для функции
y = F(x) + С.
Если во всех примерах, которые были рассмотрены выше, потребовалось бы найти множество всех первообразных, то везде следовало бы прибавить константу С.
Для функции у = (–2х + 3)3 все первообразные имеют вид:
ПРИМЕР:
По заданному закону изменения скорости тела от времени
v = –3sin 4t
найти закон движения
S = S(t),
если в начальный момент времени тело имело координату равную
1,75.
РЕШЕНИЕ:
Так как v = S'(t), нам надо найти первообразную для заданной скорости.
S = –3 1/4 (–cos 4t) + C = 3/4 cos 4t + C.
В этой задаче дано дополнительное условие – начальный момент времени. Это значит, что t = 0.
S(0)= 3/4 (–cos 4∙ 0) + C = 7/4,
Тогда закон движения описывается формулой:
S = 3/4 cos 4t + 1.
Формул для нахождения частного и произведения первообразной функции не существует.
ПРИМЕР:
Найти первообразную для функции
РЕШЕНИЕ:
Первообразной экспоненциальной функции является сама экспоненциальная функция. Первообразной исходной функции будет:
Если y = F(x) – первообразная для функции
y = f(x) на
промежутке Х, то у функции y = f(x) бесконечно много первообразных, и все они
имеют вид:
y = F(x) + С.
Если во всех примерах, которые были рассмотрены выше, потребовалось бы найти множество всех первообразных, то везде следовало бы прибавить константу С.
Для функции у = (–2х + 3)3 все первообразные имеют вид:
ПРИМЕР:
По заданному закону изменения скорости тела от времени
v = –3sin 4t
найти закон движения
S = S(t),
если в начальный момент времени тело имело координату равную
1,75.
РЕШЕНИЕ:
Так как v = S'(t), нам надо найти первообразную для заданной скорости.
S = –3 1/4 (–cos 4t) + C = 3/4 cos 4t + C.
В этой задаче дано дополнительное условие – начальный момент времени. Это значит, что t = 0.
S(0)= 3/4 (–cos 4∙ 0) + C = 7/4,
3/4 cos 0 + C = 7/4,
3/4 ∙1 + C = 7/4,
C = 1.
Тогда закон движения описывается формулой:
S = 3/4 cos 4t + 1.
Формул для нахождения частного и произведения первообразной функции не существует.
ПРИМЕР:
Найти первообразную для функции
РЕШЕНИЕ:
Так как формул для нахождения частного и
произведения первообразной функции не существует, то поступаем следующим
образом. Разобьём дробь на сумму двух дробей.
Найдём первообразные каждого слагаемого и их сумму.
F(x) = 1∙ х + ln x = х + ln x.
Решение выражений со степенью с рациональным показателем.
Многие конструкции и выражения, которые, на первый взгляд, не имеют никакого отношения к
могут быть представлены в виде степени с рациональным показателем, а именно:
ПРИМЕР:
Найдём первообразные каждого слагаемого и их сумму.
F(x) = 1∙ х + ln x = х + ln x.
Решение выражений со степенью с рациональным показателем.
Многие конструкции и выражения, которые, на первый взгляд, не имеют никакого отношения к
могут быть представлены в виде степени с рациональным показателем, а именно:
ПРИМЕР:
Посчитаем каждый корень отдельно:
Итого:
Решение задач на нахождение первообразных с заданной точкой.
Иногда необходимо из множества всех первообразных найти одну-единственную такую, которая проходила бы через заданную точку.
ПРИМЕР:
Найти первообразную для функции
f(x) = 5x4 + 6x3 – 2x + 6
РЕШЕНИЕ:
Посчитаем каждое слагаемое:
Найдём первообразную:
Эта функция должна проходить через точку М (–1; 4). Что значит, что она проходит через точку ? Это значит, что если вместо х поставить –1, а вместо F(x) – 4, то получится верное числовое равенство:
Получилось уравнение относительно С. Найдём С.
Подставим в общее решение С = 10,5 и получим ответ: ПРИМЕР:
Найти первообразную для функции
f(x) = (x – 3)2
РЕШЕНИЕ:
В первую очередь необходимо раскрыть квадрат разности по формуле сокращённого умножения.
f(x) = x2 – 6x + 9.
Посчитаем каждое слагаемое:
Найдём первообразную:
Найдём С, подставив координаты точки М.
Осталось отобразить итоговое выражение.
Решение тригонометрических задач.
ПРИМЕР:
Найти первообразную для функции
в точке М (π/4; –1).
РЕШЕНИЕ:
Воспользуемся формулой:
Тогда
F(x) = tg x + C,
Подставляем координаты точки М
–1 = tg π/4 + C,
Осталось отобразить итоговое выражение.
F(x) = tg x – 2.
ПРИМЕР:
Найти первообразную для функции
в точке М (π/4; 2).
РЕШЕНИЕ:
Воспользуемся формулой:
Или
Тогда
F(x) = –ctg x + C,
Подставляем координаты точки М
2 = –сtg (–π/4) + C,
Осталось отобразить итоговое выражение.
F(x) = –сtg x + 1.
Задания к уроку 4
Итого:
Решение задач на нахождение первообразных с заданной точкой.
Иногда необходимо из множества всех первообразных найти одну-единственную такую, которая проходила бы через заданную точку.
Все первообразные данной функции отличаются лишь тем, что они сдвинуты по
вертикали на какое-то число. А это значит, что какую бы точку на координатной
плоскости мы не взяли, обязательно пройдёт одна первообразная, и причём, только
одна.
Поэтому примеры, приведённые ниже, сформулированы следующим образом:
Надо не просто найти первообразную, зная формулу исходной функции, а
выбрать именно такую из них, которая проходит через заданную точку, координаты
которой будут даны в условии задачи.
ПРИМЕР:
Найти первообразную для функции
f(x) = 5x4 + 6x3 – 2x + 6
в точке М (–1; 4).
РЕШЕНИЕ:
Посчитаем каждое слагаемое:
Найдём первообразную:
Эта функция должна проходить через точку М (–1; 4). Что значит, что она проходит через точку ? Это значит, что если вместо х поставить –1, а вместо F(x) – 4, то получится верное числовое равенство:
Получилось уравнение относительно С. Найдём С.
Подставим в общее решение С = 10,5 и получим ответ: ПРИМЕР:
Найти первообразную для функции
f(x) = (x – 3)2
в точке М (2; –1).
РЕШЕНИЕ:
В первую очередь необходимо раскрыть квадрат разности по формуле сокращённого умножения.
f(x) = x2 – 6x + 9.
Посчитаем каждое слагаемое:
Найдём первообразную:
Найдём С, подставив координаты точки М.
Осталось отобразить итоговое выражение.
Решение тригонометрических задач.
ПРИМЕР:
Найти первообразную для функции
в точке М (π/4; –1).
РЕШЕНИЕ:
Воспользуемся формулой:
Тогда
F(x) = tg x + C,
Подставляем координаты точки М
–1 = tg π/4 + C,
–1 = 1 + C,
C = –2.
Осталось отобразить итоговое выражение.
F(x) = tg x – 2.
ПРИМЕР:
Найти первообразную для функции
в точке М (π/4; 2).
РЕШЕНИЕ:
Воспользуемся формулой:
Или
Тогда
F(x) = –ctg x + C,
Подставляем координаты точки М
2 = –сtg (–π/4) + C,
2 = сtg π/4 + C,
2 = 1 + C
C = 1.
Осталось отобразить итоговое выражение.
F(x) = –сtg x + 1.
Задания к уроку 4































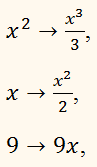








Комментариев нет:
Отправить комментарий