Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
ТЕОРЕМА КОСИНУСОВ
или посмотрите
ВИДЕО УРОК
1. В треугольнике АВС:
∠ С = 60°, АС = 8, АВ = 7.
Найдите ВС, если известно, что
ВС ˃ 4.
а) 8;
б) 6;
в) 4;
г) 5.
2.
АВ –
диаметр окружности с центром О,
который пересекает хорду СD в точке Е, лежащей на ВО. Градусная
мера дуги АС равна 60°, ОЕ = 0,6 ∙ ОА. Найдите 7 ∙ cos ∠ СEA.
а) 6;
б) 5,5;
в) 6,5;
г) 5.
3. В треугольнике АВС сторона АВ на 4 см больше стороны ВС, ∠ В = 120°, АС = 14 см. Найдите сторону АВ.
а) 10 см;
б) 12 см;
в) 8 см;
г) 14 см.
4. На стороне
АС треугольника АВС отметили точку
так, что
АВ = 14 см,
ВС = 13 см,
АС = 15 см.
а) √͞͞͞͞͞2 см;
б) 8√͞͞͞͞͞3 см;
в) 8√͞͞͞͞͞2 см;
г) √͞͞͞͞͞3 см.
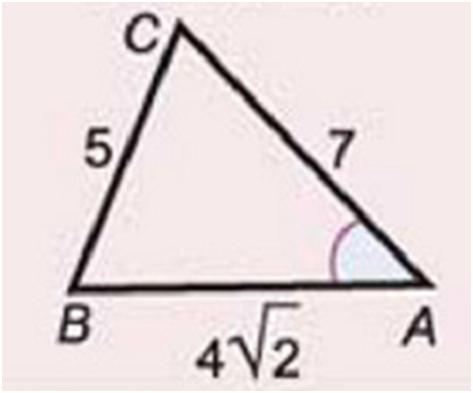
5. Для треугольника АВС известны все
стороны:
АВ = 4√͞͞͞͞͞2,
а) 45°;
б) 50°;
в) 42°;
г) 55°.
ВС = а = 4 см,
АС = b = 5
см, а
соs α = 1/2.
Необходимо найти
длину стороны АВ.
а) 2√͞͞͞͞͞23 см;
б) √͞͞͞͞͞21 см;
в) √͞͞͞͞͞23 см;
г) 2√͞͞͞͞͞21 см.
8. Для треугольника АВС известны все
стороны:
АВ = 4√͞͞͞͞͞2,
а) ≈ 78°;
б) ≈ 84°;
в) ≈ 80°;
г) ≈ 82°.
9. В треугольнике АВС стороны АС и АВ соответственно равны 7 см и 5 см, а сторона ВС = 8 см. Найдите cos А треугольника АВС.
а) –2/7;
б) 1/7;
в) –1/7;
г) 2/7.
10. В
треугольнике АВС сторона АВ на 4 см больше
стороны ВС,
∠ В = 120°, АС = 14 см.
Найдите сторону ВС.
а) 4 см;
б) 10 см;
в) 8 см;
г) 6 см.
11. Для
треугольника АВС известны все
стороны:
АВ = 4√͞͞͞͞͞2,
Найдите угол С.
а) ≈ 53°;
б) ≈ 51°;
в) ≈ 55°;
г) ≈ 50°.
12. Даны стороны
треугольника:
а = 2√͞͞͞͞͞3,
b =
3 – √͞͞͞͞͞3,
с = 3√͞͞͞͞͞2.
Вычислить угол С.
а) 135°;
б) 110°;
в) 120°;




Комментариев нет:
Отправить комментарий