ВИДЕО УРОК
Знаходження площі
фігури, обмеженої різними лініями.
Обчислення площі за
допомогою визначеного інтеграла завжди передбачає побудову креслення. Необхідно
пам'ятати графіки основних елементарних функцій і вміти будувати пряму,
параболу і гіперболу.
Обчислення площі
криволінійної трапеції.
Криволінійної
трапецією називається плоска фігура, обмежена віссю ОХ, прямими х = а, х = b і графіком безперервної на відрізку [a, b]
функції у = f (х), яка не змінює знак на цьому проміжку.
Нехай дана фігура розташована не
нижче осі абсцис.
Тоді площа криволінійної
трапеції чисельно дорівнює визначеному інтегралу
З точки зору
геометрії визначений інтеграл – це площа. Тобто, визначеному інтегралу (якщо
він існує) геометрично відповідає площа деякої фігури.
ПРИКЛАД:
Розглянемо
визначений інтеграл
підінтегральна функція
задає на площині криву, розташовану вище осі ОХ, а сам певний інтеграл
чисельно дорівнює площі відповідної криволінійної
трапеції.
ПРИКЛАД:
Обчислити площу фігури, обмеженої лініями:
у = х2 + 2,
у = 0, х = –2.
РОЗВ'ЯЗАННЯ:
Виконаємо
креслення. Спочатку краще побудувати всі прямі (якщо вони є) і тільки потім – параболи, гіперболи,
графіки інших функцій. Графіки функцій вигідніше будувати по точкам.
На відрізку [–2; 1] графік функції
у = х2 + 2
розташований
над віссю ОХ, тому:
ВІДПОВІДЬ: S = 9 ед2.
Після того, як
завдання виконано, завжди корисно подивитися на креслення і прикинути, чи
реальний вийшов відповідь. В даному випадку підраховуємо кількість клітинок в
кресленні, приблизно виходить 9. Якби вийшов відповідь приблизно 20 квадратних одиниць, то очевидно, що десь допущена
помилка – в розглянуту фігуру 20 клітинок явно не вміщається, від сили десяток. Якщо
відповідь вийшов негативним, то завдання теж вирішено неправильно.
Якщо
на відрізку [a, b] деяка безперервна функція f(x) більше або дорівнює деякій безперервній функції g(x), то площа фігури, обмеженої графіками цих функцій і прямими х = а, х = b, можна
знайти по формулі:Тут вже не потрібно думати, де розташована фігура – над віссю
або під віссю, і не важливо, який графік вищий (відносно іншого графіку), а
якої нижче.
ПРИКЛАД:
Знайти площу плоскої
фігури, обмеженої лініями:
у = 2х – х2,
у = –х.
РОЗВ'ЯЗАННЯ:
Спочатку треба виконати
креслення. При побудові креслення в завданнях на площу нас цікавлять точки
перетину ліній. Знайдемо точки перетину параболи
у = 2х – х2,
і прямій
у = –х.
це можна зробити двома
способами.
Перший спосіб –
аналітичний.
Вирішуємо рівняння:
2х – х2 = –х,
3х – х2 = 0,
х(3 – х) = 0.
х1 = 0, х2
= 3.
Означає нижню межу a = 0,
верхню межу b = 3.
Аналітичний спосіб
знаходження меж доводиться застосовувати, якщо, наприклад, графік досить
великий, або побудова по точках не виявила меж (вони можуть бути дробовими або ірраціональними).
Другий спосіб –
графічний.
Спочатку будуємо пряму і тільки потім параболу.При побудові по точках
межі інтеграції виходять <<автоматично>>.На графіці видно, що на
відрізку [0, 3] парабола розташовується
вище за пряму, а тому з 2х
– х2 необхідно відняти –х.
Завершення рішення може
виглядати так:
Шукана фігура обмежена
параболою 2х
– х2 згори і прямій –х знизу. На відрізку [0, 3]
2х – х2
≥ –х,
Тому по відповідній формулі отримуємо:ВІДПОВІДЬ:
S =
4,5 ед2.
ПРИКЛАД:
Обчислити площу фігури, обмеженої лініями:
ух = 4, х =
2,
х = 4 і віссю ОХ.
РОЗВ'ЯЗАННЯ:
Виконаємо
креслення.
На відрізку [2; 4] графік функції
у = 4/х
розташований
над віссю ОХ, тому
ВІДПОВІДЬ:
S = 4 ln 2 ед2 ≈ 2,77 ед2.
ПРИКЛАД:
Обчислити площу фігури, обмеженої лініями:
y = –ex, х = 1,
і координатними осями.
РОЗВ'ЯЗАННЯ:
Виконаємо
креслення.
Якщо криволінійна трапеція розташована під
віссю ОХ (або, по
крайній мере, не вище даної осі), то
її площа можна знайти за формулою:
В даному випадку
ВІДПОВІДЬ:
S = (е
– 1) ед2 ≈ 1,72 ед2.
Якщо необхідно вирішити просто певний інтеграл без всякого геометричного
сенсу, то він може бути негативним.
Якщо необхідно знайти площу фігури за допомогою певного інтеграла, то
отриманий результат повинен бути завжди позитивним.
Обчислення об'єму тіла обертання.
Знайдемо формулу для обчислення обсягу будь-якого
тіла обертання.
Проведемо площину через
вісь тіла і введемо в цій площині Декартові координати х, y прийнявши вісь тіла за вісь х. Площина
ху перетинає поверхню тіла
по лінії, для якої вісь х є віссю
симетрії.
Нехай y = (х)
– рівняння тієї частини цієї лінії, яка розташована над віссю х. Проведемо через
точку (х, 0)
площину,
перпендикулярну осі х,
і позначимо через V(x) обсяг частини тіла, яка
лежить ліворуч від цієї площини, V(x)
є
функцією від х. Різниця
V(x + h)
– V(x)
являє
собою обсяг прошарку тіла товщиною h, заключеного між двома площинами,
які перпендикулярні осі х і проходять через точки з
абсцисами х і х + h. Нехай М – більше, а m – найменше значення функції f (х) на відрізку [x, x + h]. Тоді
розглянута прошарок тіла містить циліндр з радіусом m і висотою h і знаходиться в циліндрі з радіусом М і тієї ж висотою h. Тому
При
прагненні висоти h до нуля ліва і права частини
останнього нерівності прагнуть до однієї і тієї ж величині πf 2 (x). Середня ж частина цієї нерівності
при прагненні h до 0 прагне до похідної
V' (x)
функції V(x). Виходить,
V' (x) = πf
2 (x).
За відомою формулою
Ця формула і дає обсяг частини тіла, укладеного між
паралельними площинами х = а і х = b.
Алгоритм
обчислення обсягів геометричних тіл за допомогою визначеного інтеграла
1. Ввести систему координат так, що вісь ОХ перпендикулярна основи геометричного тіла.
2. Знайти границі інтегрування а и b.
3. Провести розтин площиною перпендикулярно осі ОХ через точку з абсцисою х.
4. Визначити вид перетину, задати формулою його
площа як функцію S(Х).
5. Перевірити
безперервність функції S(Х) на [a; b].
ЗАДАЧА:
Знайти
об’єм тіла, утвореного обертанням фігури, обмеженої лініями
навколо осі ординат.
РОЗВ'ЯЗАННЯ:
Зобразимо вказане тіло обертання:
Тоді шуканий об’єм
дорівнює:
ВІДПОВІДЬ:
V0у = 8π (куб. ед.)
Обчислення
площі поверхні тіла.
Нехай крива АВ
задана функцією
y
= f (x) ≥ 0, x ∈ [a; b],
яка є безперервною разом
зі своєю похідною y'(x) на цьому відрізку. Площа
S поверхні
утвореної обертанням кривої АВ навколо
осі Ох дорівнює
ЗАДАЧА:
Знайти площу поверхні кулі з центром на початку
координат радіуса R.
РОЗВ'ЯЗАННЯ:
Будемо вважати, що поверхня кулі утворена
обертанням півкола
навколо осі абсцис.
Тоді за формулою знаходимо, що шукана площа
дорівнює:
ВІДПОВІДЬ:
SОх = 4πR2 (кв. ед.)
Завдання до уроку 8
Інші уроки:









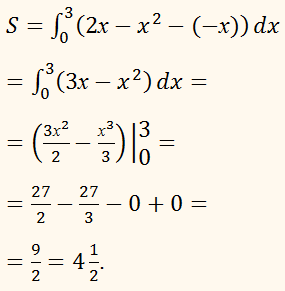















Комментариев нет:
Отправить комментарий