Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
РІШЕННЯ ЗАВДАНЬ ЗА ДОПОМОГОЮ ВЕКТОРІВ
або
ВІДЕО УРОК
1. Знайдіть кут між сторонами АС і медіаною ВМ трикутника АВС, якщо
А(–3;
–5; 1),
В(–4;
–1; –2),
С(3;
3; 1).
а) arccos
11/25;
б) arccos 14/25;
в) arccos 12/25;
г) arccos 8/25.
б) 36;
в) 16;
г) 22.
б) (1; 1; –1);
в) (1; –1; 1);
г) (–1; 1; 1).
б) (1; 1; –1);
в) (1; –1; 1);
г) (–1; 1; 1).
DM : MC1 =
5 : 3.
АЕ : ЕD1 = 2 : 7.
7. Відрізок СЕ – медіана грані ВМС піраміди МАВС, точка К – середина відрізка СЕ.Виразіть вектор 8. На стороні АD паралелограма АВСD, зображеного на рисунку,позначили точку Е, а на стороні СD – точку F так, щоАЕ
: ЕD = 3 : 1,
Чому дорівнює модуль вектора: а) 2√͞͞͞͞͞3;
б) 2;
в) √͞͞͞͞͞3;
г) 1.
10. Чотирикутник ABCD – паралелограм,
B(4;
1), C(–1; 1), D(–2; –2).
Знайдіть координати вершини А.
а) А(–3;
–2);
б) А(3; –2);
в) А(3;
2);
г) А(–3;
2).
11.
Чотирикутник ABCD – паралелограм,
А(–4; 4), В(–1; 5), D(–5; 1).
Знайдіть координати вершини C.
а) С(–2;
–2);
б) С(2; –2);
в) С(2;
2);
г) С(–2; 2).
12. На
сторонах BC і CD
паралелограма АВСD позначено відповідно точки M і N
так, що
BM
: MC = 2 : 3,





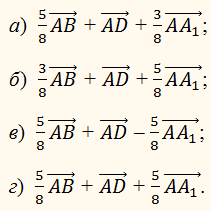












Комментариев нет:
Отправить комментарий